题目内容
倾听理解:
这是一次数学活动课上,两个同学利用计算机软件探索函数问题,下面是他们的交流片断:

问题解决:
(1)填空:图②中,小苏发现的
= ;
(2)记图①,图②中MN为d1,d2,分别求出d1,d2与m之间的函数关系式.
拓广探索:
(3)如图③,直线x=m(m>0)分别交x轴,抛物线y=x2-4x和y=x2-3x于点P,M,N,设A,B为抛物线y=x2-4x,y=x2-3x与x轴的另一交点.当m为何值时,线段OP,PM,PN,MN中有三条能围成等边三角形?并直接写出此时点A,B,M,N围成的图形的面积.

这是一次数学活动课上,两个同学利用计算机软件探索函数问题,下面是他们的交流片断:

问题解决:
(1)填空:图②中,小苏发现的
| MN |
| PM |
(2)记图①,图②中MN为d1,d2,分别求出d1,d2与m之间的函数关系式.
拓广探索:
(3)如图③,直线x=m(m>0)分别交x轴,抛物线y=x2-4x和y=x2-3x于点P,M,N,设A,B为抛物线y=x2-4x,y=x2-3x与x轴的另一交点.当m为何值时,线段OP,PM,PN,MN中有三条能围成等边三角形?并直接写出此时点A,B,M,N围成的图形的面积.

考点:二次函数综合题
专题:
分析:(1)把当x=m分别代入反比例函数的解析式,求出M点的纵坐标和N点的纵坐标,进而求出MN的长,则
值可求出;
(2)当x=m时,则M点的纵坐标为m,N点的纵坐标为2m,进而求出MN的长,d1可求,同理可求出d2;
(3)由函数的解析式分别求出PM,PN,MN的长,根据等边三角形的性质:三边相等即可求出m的值,利用梯形的性质即可求出其面积.
| MN |
| PM |
(2)当x=m时,则M点的纵坐标为m,N点的纵坐标为2m,进而求出MN的长,d1可求,同理可求出d2;
(3)由函数的解析式分别求出PM,PN,MN的长,根据等边三角形的性质:三边相等即可求出m的值,利用梯形的性质即可求出其面积.
解答:解:(1)当x=m时,
则M点的纵坐标为
,N点的纵坐标为
,
所以MN=
-
=
,
∴
=
=
,
故答案为:
;
(2)当x=m时,则M点的纵坐标为m,N点的纵坐标为2m,
∴MN=2m-m=m,
即d1=m,
当x=m时,则M点的纵坐标为
,N点的纵坐标为
,
∴MN=
-
=
,
即d2=
;
(3)OP=m,PM=|4m-m2|=m|4-m|,PN=|3m-m2|=m|3-m|,MN=m,
由题意,得m|4-m|=m或m|3-m|=m,
解得m=5或m=3或m=4或m=2,
当m=3时,点P与点A重合,当m=4时,点P与点B重合,
所以,m=2或5,
当m=2时,S=3;当m=5时,S=7.5.
则M点的纵坐标为
| 2 |
| m |
| 3 |
| m |
所以MN=
| 3 |
| m |
| 2 |
| m |
| 1 |
| m |
∴
| MN |
| PM |
| ||
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(2)当x=m时,则M点的纵坐标为m,N点的纵坐标为2m,
∴MN=2m-m=m,
即d1=m,
当x=m时,则M点的纵坐标为
| 2 |
| m |
| 3 |
| m |
∴MN=
| 3 |
| m |
| 2 |
| m |
| 1 |
| m |
即d2=
| 1 |
| m |
(3)OP=m,PM=|4m-m2|=m|4-m|,PN=|3m-m2|=m|3-m|,MN=m,
由题意,得m|4-m|=m或m|3-m|=m,
解得m=5或m=3或m=4或m=2,
当m=3时,点P与点A重合,当m=4时,点P与点B重合,
所以,m=2或5,
当m=2时,S=3;当m=5时,S=7.5.
点评:本题考查了一次函数、反比例函数、二次函数的各种性质以及等边三角形的性质和梯形的面积公式的,题目的综合性较强,对学生的解题能力要求很高.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
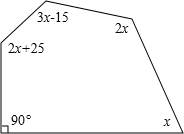 如图所示,请你根据图中信息求出x的值.
如图所示,请你根据图中信息求出x的值.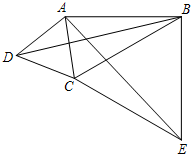 如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE. 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.