题目内容
14.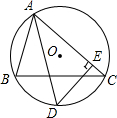 如图,⊙O为△ABC的外接圆,$\widehat{BD}$=$\widehat{CD}$,DE⊥AC于E,AB=4,AC=6,求CE的长.
如图,⊙O为△ABC的外接圆,$\widehat{BD}$=$\widehat{CD}$,DE⊥AC于E,AB=4,AC=6,求CE的长.
分析 作DF⊥AB于F,如图,根据圆周角定理由$\widehat{BD}$=$\widehat{CD}$得∠BAD=∠CADDB=DC,再根据角平分线的性质得DF=DE,接着利用“HL”证明Rt△DBF≌Rt△DCE得BF=CE,证明Rt△DAF≌Rt△DAE得AF=AE,则有AB+BF=AC-CE,然后计算CE的长.
解答 解:作DF⊥AB于F,如图,
∵$\widehat{BD}$=$\widehat{CD}$,
∴DB=DC,∠BAD=∠CAD,
∴AD平分∠BAC,
∵DE⊥AC,DF⊥AB,
∴DF=DE,
在Rt△DBF和Rt△DCE中
$\left\{\begin{array}{l}{DB=DC}\\{DF=DE}\end{array}\right.$,
∴Rt△DBF≌Rt△DCE,
∴BF=CE,
在Rt△DAF和Rt△DAE中
$\left\{\begin{array}{l}{AD=AD}\\{DF=DE}\end{array}\right.$,
∴Rt△DAF≌Rt△DAE,
∴AF=AE,
即AB+BF=AC-CE,
∴4+CE=6-CE,
∴CE=1.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了全等三角形的判定与性质和角平分线的性质.本题的关键是作辅助线构建全等三角形.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,求∠A的度数.
如图,在Rt△ABC中,∠C=90°,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,求∠A的度数. 如图,△ABC中,AB=AC=10cm,S△ABC=40cm2,点D为BC边上任意一点,设点D到AB、AC的距离分别为DE=acm,DF=bcm.
如图,△ABC中,AB=AC=10cm,S△ABC=40cm2,点D为BC边上任意一点,设点D到AB、AC的距离分别为DE=acm,DF=bcm.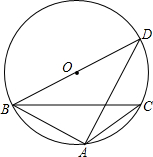 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,求AC的长.
如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,求AC的长.