ĖâÄŋÄÚČÝ
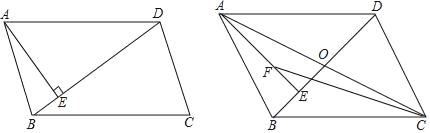
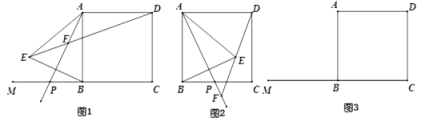
ĄūĖâÄŋĄŋķĻŌåĢšČôŌŧļöËÄąßÐÎÄÜąŧÆäÖÐŌŧĖõķÔ―ĮÏß·ÖļîģÉÁ―ļöÏāËÆČý―ĮÐÎĢŽÔōģÆÕâļöËÄąßÐÎΊĄ°ÓŅšÃËÄąßÐÎĄąĢŪ
ĢĻ1ĢĐČįÍž1ĢŽÔÚ![]() ĩÄÕý·―ÐÎÍøļņÖÐĢŽÓÐŌŧļöÍøļņ
ĩÄÕý·―ÐÎÍøļņÖÐĢŽÓÐŌŧļöÍøļņ![]() šÍÁ―ļöÍøļņËÄąßÐÎ
šÍÁ―ļöÍøļņËÄąßÐÎ![]() Óë
Óë![]() ĢŽÆäÖÐĘĮąŧ
ĢŽÆäÖÐĘĮąŧ![]() ·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĩÄĘĮ Ģŧ
·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĩÄĘĮ Ģŧ
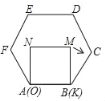
ĢĻ2ĢĐČįÍž2ĢŽ―Ŧ![]() ČÆĩã
ČÆĩã![]() ÄæĘąÕëÐýŨŠĩÃĩ―
ÄæĘąÕëÐýŨŠĩÃĩ―![]() ĢŽĩã
ĢŽĩã![]() ÂäÔÚąß
ÂäÔÚąß![]() ĢŽđýĩã
ĢŽđýĩã![]() Ũũ
Ũũ![]() ―ŧ
―ŧ![]() ĩÄŅÓģĪÏßÓÚĩã
ĩÄŅÓģĪÏßÓÚĩã![]() ĢŽĮóÖĪĢšËÄąßÐÎ
ĢŽĮóÖĪĢšËÄąßÐÎ![]() ĘĮĄ°ÓŅšÃËÄąßÐÎĄąĢŧ
ĘĮĄ°ÓŅšÃËÄąßÐÎĄąĢŧ
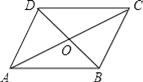
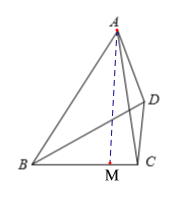
ĢĻ3ĢĐČįÍž3ĢŽÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĩÄÃæŧýΊ
ĩÄÃæŧýΊ![]() ĢŽĩã
ĢŽĩã![]() ĘĮ
ĘĮ![]() ĩÄÆ―·ÖÏßÉÏŌŧĩãĢŽÁŽ―Ó
ĩÄÆ―·ÖÏßÉÏŌŧĩãĢŽÁŽ―Ó![]() ĢŽ
ĢŽ![]() ĢŪČôËÄąßÐÎ
ĢŪČôËÄąßÐÎ![]() ĘĮąŧ
ĘĮąŧ![]() ·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĢŽĮó
·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĢŽĮó![]() ĩÄģĪĢŪ
ĩÄģĪĢŪ
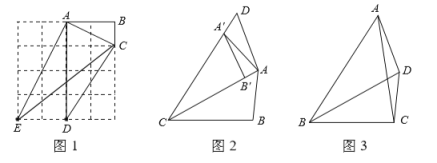
Ąūīð°ļĄŋĢĻ1ĢĐËÄąßÐÎ![]() ĢŧĢĻ2ĢĐÏęžû―âÎöĢŧĢĻ3ĢĐ
ĢŧĢĻ2ĢĐÏęžû―âÎöĢŧĢĻ3ĢĐ![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝČý―ĮÐÎÏāËÆĩÄÅÐķĻķĻĀíĢŽĩÃABC~EACĢŽ―øķøžīŋÉĩÃĩ―īð°ļĢŧ
ĢĻ2ĢĐÓÉÐýŨŠĩÄÐÔÖĘĩÃĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ―ášÏ
ĢŽ―ášÏ![]() ĢŽĩÃ
ĢŽĩÃ![]() ĢŽ―øķøžīŋÉĩÃĩ――áÂÛĢŧ
ĢŽ―øķøžīŋÉĩÃĩ――áÂÛĢŧ
ĢĻ3ĢĐđýĩã![]() Ũũ
Ũũ![]() ÓÚ
ÓÚ![]() ĢŽĩÃ
ĢŽĩÃ![]() ĢŽļųūÝČý―ĮÐÎĩÄÃæŧýĩÃ
ĢŽļųūÝČý―ĮÐÎĩÄÃæŧýĩÃ![]() ĢŽ―ášÏ
ĢŽ―ášÏ![]() ĄŨ
ĄŨ![]() ĢŽžīŋÉĩÃĩ―īð°ļĢŪ
ĢŽžīŋÉĩÃĩ―īð°ļĢŪ
ĢĻ1ĢĐÓÉĖâŌâĩÃĢš![]() ,
,
Ąā![]() ĢŽ
ĢŽ
ĄāABC~EACĢŽ
Ąāąŧ![]() ·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĩÄĘĮĢšËÄąßÐÎ
·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĩÄĘĮĢšËÄąßÐÎ![]() ĢŽ
ĢŽ
đĘīð°ļĘĮĢšËÄąßÐÎ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐļųūÝÐýŨŠĩÄÐÔÖĘĩÃĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
Ąß![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĄŨ
ĄŨ![]() ĢŽ
ĢŽ
ĄāËÄąßÐÎ![]() ĘĮĄ°ÓŅšÃËÄąßÐÎĄąĢŧ
ĘĮĄ°ÓŅšÃËÄąßÐÎĄąĢŧ
ĢĻ3ĢĐđýĩã![]() Ũũ
Ũũ![]() ÓÚ
ÓÚ![]() ĢŽ
ĢŽ
ĄāÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
Ąß![]() ĩÄÃæŧýΊ
ĩÄÃæŧýΊ![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄßËÄąßÐÎ![]() ĘĮąŧ
ĘĮąŧ![]() ·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĢŽĮŌ
·ÖļîģÉĩÄĄ°ÓŅšÃËÄąßÐÎĄąĢŽĮŌ![]() ĢŽ
ĢŽ
Ąā![]() ĄŨ
ĄŨ![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĢŪ
ĢŪ

 ÐĄŅ§ŋÎĘąĖØŅĩÏĩÁÐīð°ļ
ÐĄŅ§ŋÎĘąĖØŅĩÏĩÁÐīð°ļ