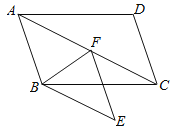
��Ŀ����
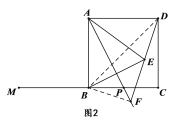
����Ŀ����ͼ����֪�߶�![]() ��
�� ![]() ��
��![]() �ϵ�һ���㣬
�ϵ�һ���㣬![]() ��
��![]() ���е㣬��
���е㣬��![]() Ϊ����������
����������![]() ����
����![]() ��������
��������![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
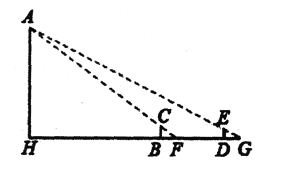
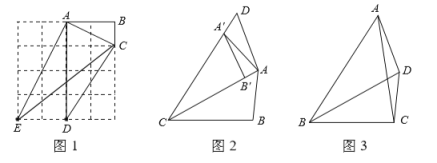
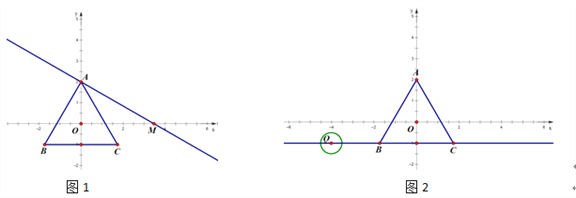
��1����ͼ1������![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ����
����![]() �Ķ�����
�Ķ�����
��2��С���ڽ���ʱ���֣�����![]() ���߶�
���߶�![]() ��ʱ���߶�
��ʱ���߶�![]() ��
��![]() ��
��![]() ֮������
֮������![]() ����ô����Ϊ����
����ô����Ϊ����![]() ���߶�
���߶�![]() ��ʱ����ͼ2�������Ľ����Ƿ���������������֤����������������˵�����ɣ�
��ʱ����ͼ2�������Ľ����Ƿ���������������֤����������������˵�����ɣ�
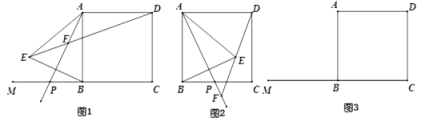
��3����ͼ3����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ʱ��ֱ��д����
ʱ��ֱ��д����![]() ��������·������
��������·������
���𰸡���1����AFD=45 ����2�����������ɼ���������3����![]() ��������·����Ϊ
��������·����Ϊ![]() ��
��
��������
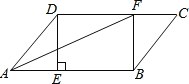
��1�����ݵ�![]() ��������
��������![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ���ó�AE=AB����EAP=��PAB=25���ٸ��������κ͵��������ε����ʵó���AED��Ȼ����������ε���Ǽ��ɵó�����
���ó�AE=AB����EAP=��PAB=25���ٸ��������κ͵��������ε����ʵó���AED��Ȼ����������ε���Ǽ��ɵó�����
��2������BF��BD���ȸ��������ε����ʿɵ�BD=2AD���ٸ��������ε���Ǻ��ڽǺͶ����ó���AFD=45����ȷ��BFD ��ֱ�������Σ����ɵó�����
��3������P�˶�����Qʱ��BP=2����ֱ����������ABP���ó���BAP=30���ٸ�����AFD=![]() ��AOD���ɵõ�F��������·����Ϊ�Ե�OΪԲ�ģ���OA��Ϊ�뾶��Բ�Ľ���AOF=150�Ļ��������������
��AOD���ɵõ�F��������·����Ϊ�Ե�OΪԲ�ģ���OA��Ϊ�뾶��Բ�Ľ���AOF=150�Ļ��������������
��1��֤�������ı���ABCD��������
��AB=AD����BAD=90
����B���E��������AP�Գ�
��AE=AB����EAP=��PAB=25
��AE=AD����EAD=��EAB+��BAD=140
���AED=![]() (180-��EAD)=
(180-��EAD)= ![]() (180-140)=20
(180-140)=20
���AFD=��AED+��EAP=20+25=45
��2������
�������£�����BF��BD��
��RtABD��BD=AB+AD=2AD
����B���E��������AP�Գ�
��BF=EF ��AB=AE=AD����AFB=��AFD
���BAF=��EAF����ADE=��AED
�ߡ�AED����AEF�����
���AED=��EAF+��AFD
���ߡ�DAE=90��2��EAF
������ADE����DAE+��ADE+��AED=180
��90��2��EAF+2(��EAF+��AFD)=180
���AFD=45
���BFD=2��AFD=90
����RtBFD��B F+DF=BD
��EF+DF=2AD
��3����![]() ��������·����Ϊ
��������·����Ϊ![]() ��
��

��AC��BD�ཻ�ڵ�O����
OA=![]() AB=
AB=![]()
���ڵ�F���˶������У���AFD=45
���AFD=![]() ��AOD
��AOD
����P�˶�����Qʱ��BP=2
��Rt��ABP��tan��BAP=![]()
���BAP=30���CAF=15
����F��������·����Ϊ�Ե�OΪԲ�ģ���OA
����F��������·����Ϊ![]() ��
��

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�