题目内容
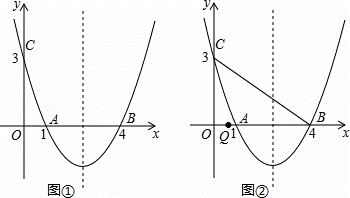
如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
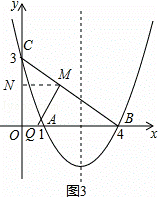
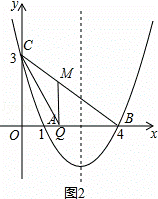
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
解:(1)由已知得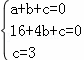 解得
解得 .
.
所以,抛物线的解析式为y=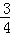 x2﹣
x2﹣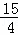 x+3.
x+3.
(2)∵A、B关于对称轴对称,如图1,连接BC,
∴BC与对称轴的交点即为所求的点P,此时PA+PC=BC,
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=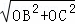 =5,
=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9.
(3)∵B(4,0)、C(0,3),
∴直线BC的解析式为y=﹣ x+3,
x+3,
①当∠BQM=90°时,如图2,设M(a,b),
∵∠CMQ>90°,
∴只能CM=MQ=b,
∵MQ∥y轴,
∴△MQB∽△COB,
∴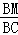 =
=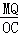 ,即
,即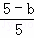 =
=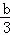 ,解得b=
,解得b= ,代入y=﹣
,代入y=﹣ x+3得,
x+3得, =﹣
=﹣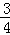 a+3
a+3 ,解得a=
,解得a=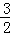 ,
,
∴M(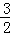 ,
,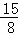 );
);
②当∠QMB=90°时,如图3,
∵∠CMQ=90°,
∴只能CM=MQ,
设CM=MQ=m,
∴BM=5﹣m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,
∴△BMQ∽△BOC,
∴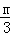 =
=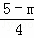 ,解得m=
,解得m=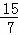 ,
,
作MN∥OB,
∴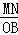 =
=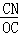 =
= ,即
,即 =
=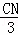 =
=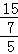 ,
,
∴MN=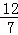 ,CN=
,CN=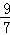 ,
,
∴ON=OC﹣CN=3﹣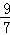 =
=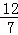 ,
,
∴M(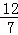 ,
,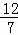 ),
),
综上,在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为(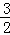 ,
,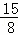 )或(
)或(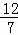 ,
,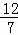 ).
).


 综合自测系列答案
综合自测系列答案甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
|
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 )
)

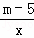 (m为常数,且m≠5).
(m为常数,且m≠5).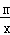 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.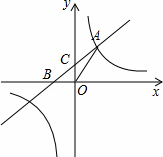






 的公差
的公差 ,它的前
,它的前 项和为
项和为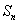 ,若
,若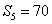 ,且
,且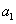 ,
,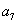 ,
,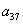 成等比数列.
成等比数列.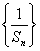 的前
的前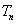 ,求证:
,求证: .
.