题目内容
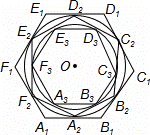
如图，正六边形A1B1C1D1E1F1的边长为2，正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切，正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切，…按这样的规律进行下去，A10B10C10D10E10F10的边长为（ ）
|
| A． |
| B． |
| C． |
| D． |
|
D解：连结OE1，OD1，OD2，如图，
∵六边形A1B1C1D1E1F1为正六边形，
∴∠E1OD1=60°，
∴△E1OD1为等边三角形，
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切，
∴OD2⊥E1D1，
∴OD2=
E1D1=×2，
∴正六边形A2B2C2D2E2F2的边长=×2，
同理
可得正六边形A3B3C3D3E3F3的边长=（）2×2，
则正六边形A10B10C10D10E10F10的边长=（）9×2=
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
中，
，连接
，且
°,
，
，则
．
=
=
=
=
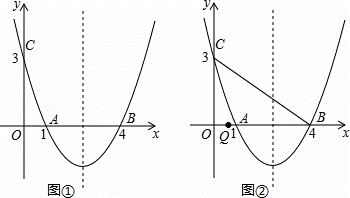
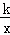（k≠0）的图象交于点A，B，直线y=k2x与反比例函数y=
的二项式
展开式中的常数项是