题目内容
已知等差数列 的公差
的公差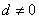 ,它的前
,它的前 项和为
项和为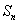 ,若
,若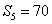 ,且
,且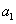 ,
,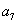 ,
,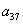 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设数列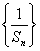 的前
的前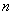 项和为
项和为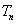 ,求证:
,求证: .
.
(1)解:因为数列 是等差数列,
是等差数列,
所以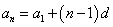 ,
,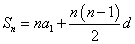 . …………………………………1分
. …………………………………1分
依题意,有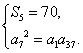 即
即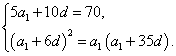 …………………3分
…………………3分
解得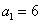 ,
,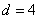 . ………………………………………………………………5分
. ………………………………………………………………5分
所以数列 的通项公式为
的通项公式为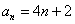 (
(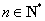 ). …………………………6分
). …………………………6分
(2)证明:由(1)可得
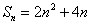 . …………………………………………7分
. …………………………………………7分
所以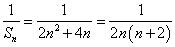
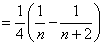 . …………………………8分
. …………………………8分
所以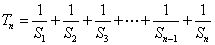
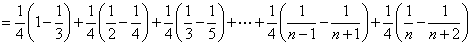 ……9分
……9分
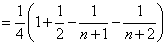
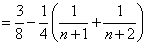 . …………………………………………………10分
. …………………………………………………10分
因为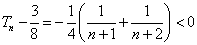 ,所以
,所以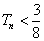 . …………………………11分
. …………………………11分
因为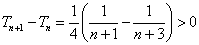 ,
, 所以数列
所以数列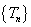 是递增数列. …………12分
是递增数列. …………12分
所以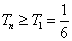 . …………………………………………………………………13分
. …………………………………………………………………13分
所以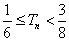 . …………………………………………………………………14分
. …………………………………………………………………14分

练习册系列答案
相关题目
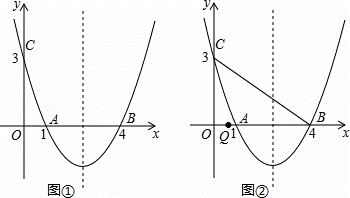

 表示的平面区域的面积为
表示的平面区域的面积为 ,则实数
,则实数 的值为
的值为 B.
B. D.
D.

 中,
中, 的值是( )
的值是( )  的二项式
的二项式 展开式中的常数项是
展开式中的常数项是 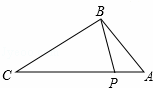
 =
=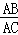 D.
D. 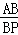 =
=