题目内容
已知直线y=x+m和双曲线 的一个交点为(α,β).其中α<β,并且α,β是方程2x2-4x+1=0的两个实数根,求这两图象的解析式.
的一个交点为(α,β).其中α<β,并且α,β是方程2x2-4x+1=0的两个实数根,求这两图象的解析式.
【答案】分析:此题通过求交点坐标解题,较繁,用根与系数关系比较简单,把交点坐标(α,β)代入两解析式,并变形,得m=β-α,k=αβ,∵α,β是方程2x2-4x+1=0的根,根据根与系数的关系不难算出m,k的值.
解答:解:∵直线y=x+m和双曲线 的一个交点为(α,β),
的一个交点为(α,β),
∴β=α+m,k=αβ,即m=β-α,k=αβ,
∵α,β是方程2x2-4x+1=0的根,∴α+β=2,αβ= =k,
=k,
∴(β-α)2=(α+β)2-4αβ=4-2=2,∴β-α= 或β-α=-
或β-α=- ,
,
∵α<β,∴β-α= ,即m=β-α=
,即m=β-α= ,αβ=
,αβ= =k,
=k,
∴两图象的解析式为: ,
, .
.
点评:本题考查了反比例函数与一次函数的交点及根与系数的关系,难度适中,关键是掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.
解答:解:∵直线y=x+m和双曲线
 的一个交点为(α,β),
的一个交点为(α,β),∴β=α+m,k=αβ,即m=β-α,k=αβ,
∵α,β是方程2x2-4x+1=0的根,∴α+β=2,αβ=
 =k,
=k,∴(β-α)2=(α+β)2-4αβ=4-2=2,∴β-α=
 或β-α=-
或β-α=- ,
,∵α<β,∴β-α=
 ,即m=β-α=
,即m=β-α= ,αβ=
,αβ= =k,
=k,∴两图象的解析式为:
 ,
, .
.点评:本题考查了反比例函数与一次函数的交点及根与系数的关系,难度适中,关键是掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
相关题目
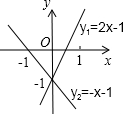 已知直线y1=2x-1和y2=-x-1的图象如图所示,根据图象填空.当x
已知直线y1=2x-1和y2=-x-1的图象如图所示,根据图象填空.当x 如图,已知直线y=kx+3和直线y=mx-2交于点P(-2,1),则方程组
如图,已知直线y=kx+3和直线y=mx-2交于点P(-2,1),则方程组