题目内容
11.已知二次函数y=$\frac{1}{2}$x2-2的图象与x轴交于A、B两点,与y轴交于C点.(1)求A、B、C点的坐标;
(2)判断△ABC的形状,并求其面积.
分析 (1)令y=0,可得出关于x的一元二次方程,解方程即可得出点A、B的坐标,令x=0求出y值,由此即可得出点C的坐标;
(2)利用两点间的距离公式可得出AC、BC、AB的长度,结合AB2=AC2+BC2且AC=BC即可得出△ABC为等腰直角三角形,再根据三角形的面积公式求出△ABC的面积即可得出结论.
解答 解:(1)令y=0,则$\frac{1}{2}$x2-2=0,
解得:x1=-2,x2=2,
∴A(-2,0)、B(2,0)或A(2,0)、B(-2,0);
令x=0,y=-2,
∴C点的坐标为(0,-2).
(2)∵A(-2,0)、B(2,0)或A(2,0)、B(-2,0),且C(0,-2),
∴AC=2$\sqrt{2}$,BC=2$\sqrt{2}$,AB=4,
∴AB2=AC2+BC2.
∵AC=BC,
∴△ABC为等腰直角三角形.
S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$=4.
点评 本题考查了抛物线与x轴的交点坐标、二次函数图象上点的坐标特征、等腰直角三角形的判定以及三角形的面积,根据二次函数图象上点的坐标特征求出点A、B、C的坐标是解题的关键.

练习册系列答案
相关题目
1.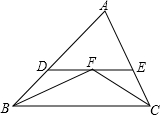 如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①∠A=2∠BFC-180°;②DE-BD=CE;③△ADE的周长等于AB与AC的和;④BF>CF.
其中正确的有( )
 如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①∠A=2∠BFC-180°;②DE-BD=CE;③△ADE的周长等于AB与AC的和;④BF>CF.
其中正确的有( )
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
2. 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )| A. | 2.5m | B. | 3m | C. | 3.5m | D. | 4m |
19.将正偶数按表格方式排成5列若干行:
根据上述规律,数2016应在( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … | … |
| A. | 第251行 第1列 | B. | 第251行 第5列 | C. | 第252行 第4列 | D. | 第252行 第1列 |
16.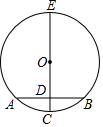 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
①AD=BD;②$\widehat{AC}$=$\widehat{BC}$;③$\widehat{AE}$=$\widehat{BE}$;④OD=CD.
 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )①AD=BD;②$\widehat{AC}$=$\widehat{BC}$;③$\widehat{AE}$=$\widehat{BE}$;④OD=CD.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.若x=-1是关于x的方程2x+m=1的解,则m-1的值是( )
| A. | 3 | B. | 2 | C. | -2 | D. | -1 |
20.已知am=9,am-2n=3,则an的值是( )
| A. | -3 | B. | $\sqrt{3}$ | C. | $\frac{1}{3}$ | D. | ±$\sqrt{3}$ |
1.下列数中与-2互为倒数的是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于A、B两点,且与反比例函数y=$\frac{k_2}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OA=OB=2,OD=1.