Question

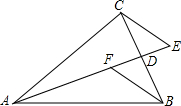如图，在△ABC中，AD为BC边中线，作CE⊥AC于C，交AD延长线于点E，过点B作BF∥CE交AD于点F．
（1）求证：DE=DF；
（2）若AD=DE+2BD，∠ABC=∠DCE+∠BAC，求证：
①AD⊥BC；
②CE=（

2

-1）AB．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）由AD是△ABC的中线就可以得出BD=CD，再由平行线的性质就可以得出△CDE≌△BDF就可以得出DE=DF．
（2）①作FM∥AC交AB于M，延长BF交AC于N，延长CD交AB于G，根据已知条件和平行线的性质求得∠MFB=90°AN=BN，然后根据HL求得RT△AND≌RT△BNC，求得∠NAD=∠CBN，进而求得∠DFB+∠NBC=90°，进而求得AD⊥BC；
②先求得△MFB是等腰直角三角形，得出FM=FB，然后根据垂直平分线的性质得出AB=AC，进而求得∠DAB=∠DAC，再根据平行线的性质求得∠AFM=∠DAB，得出AM=FM=BF，根据ASA求得△CDE≌△BDF得出CE=BF，进而求得AM=CE，BM=

2

CE，即可求得结论．

解答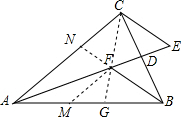：证明：∵AD是BC的中线，
∴BD=CD．
∵BF∥CE，
∴∠ECD=∠FBD，∠DEC=∠DFB．
在△CDE和△BDF中

∠ECD=∠FBD ∠DEC=∠DFB CD=BD

，
∴△CDE≌△BDF（AAS），
∴DE=DF．

（2）作FM∥AC交AB于M，延长BF交AC于N，延长CD交AB于G，
∴∠MFB=∠ANB，
∵BF∥EC，
∴∠ANB=∠ACE=90°，
∴∠MFB=∠ACE=90°，
∵AD=DE+2BD，
∵BD=DC，DE=DF，
∴AF=BC，
∵∠CAB=∠NBA，
∵∠ABC=∠DCE+∠BAC，∠FBC=∠ECB，
∴∠ABN=∠BAC，
∵AN=BN，
在RT△AND与RT△BNC中，

AF=CB AN=NB

，
∴RT△AND≌RT△BNC（HL），
∴∠NAD=∠CBN，
∵∠NFA=∠DFB，∠NFA+∠NAD=90°，
∴∠DFB+∠NBC=90°，
∴∠FDB=90°，
∴AD⊥BC，
②∵AD垂直平分BC，
∴AB=AC，
∴∠DAB=∠DAC，
∵FM∥AC，
∴∠CAD=∠AFM，
∴∠AFM=∠DAB，∠DNB=∠CAB=45°
∴AM=FM=BF，
在△CDE与△BDF中，

∠FBC=∠ECB CD=BD ∠CDE=∠BDF

∴△CDE≌△BDF（ASA），
∴CE=BF，
∵在等腰直角三角形MFB中，MB=

2

BF=

2

CE，∴AB=AM+MB=CE+

2

CE=（1+

2

）CE，
∴CE=（

2

-1）AB．

点评：本题考查了三角形的中线的性质的运用，平行线的性质的运用，全等三角形的判定及性质的运用，等腰直角三角形性质的运用，解答时证明三角形全等是关键．