题目内容
4.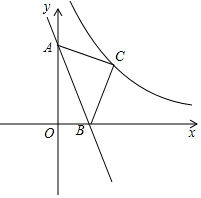 如图,在平面直角坐标系中,将直线y=-3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,求此反比例函数的表达式.
如图,在平面直角坐标系中,将直线y=-3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,求此反比例函数的表达式.
分析 过点C作CE⊥x轴于点E,作CF⊥y轴于点F,根据等腰直角三角形的性质可证出△ACF≌△BCE(AAS),从而得出S矩形OECF=S四边形OBCA=S△AOB+S△ABC,根据直线AB的表达式利用一次函数图象上点的坐标特征可得出点A、B的坐标,结合勾股定理可得出AB的长度,再根据三角形的面积结合反比例函数系数k的几何意义,即可求出k值,此题得解.
解答 解:过点C作CE⊥x轴于点E,作CF⊥y轴于点F,如图所示.
∵CE⊥x轴,CF⊥y轴,
∴∠ECF=90°.
∵△ABC为等腰直角三角形,
∴∠ACF+∠FCB=∠FCB+∠BCE=90°,AC=BC,
∴∠ACF=∠BCE.
在△ACF和△BCE中,$\left\{\begin{array}{l}{∠AFC=∠BEC=90°}\\{∠ACF=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△ACF≌△BCE(AAS),
∴S△ACF=S△BCE,
∴S矩形OECF=S四边形OBCA=S△AOB+S△ABC.
∵将直线y=-3x向上平移3个单位可得出直线AB,
∴直线AB的表达式为y=-3x+3,
∴点A(0,3),点B(1,0),
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{10}$,
∵△ABC为等腰直角三角形,
∴AC=BC=$\sqrt{5}$,
∴S矩形OECF=S△AOB+S△ABC=$\frac{1}{2}$×1×3+$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=4.
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,
∴k=4,
∴此反比例函数的表达式为y=$\frac{4}{x}$.
点评 本题考查了反比例函数系数k的几何意义、全等三角形的判定与性质、一次函数图象上点的坐标特征、一次函数图象与几何变换、等腰直角三角形以及三角形的面积,根据等腰直角三角形的性质结合角的计算,证出△ACF≌△BCE(AAS)是解题的关键.

 名校课堂系列答案
名校课堂系列答案①两条直线被第三条直线所截,同位角相等
②经过直线外一点,有且只有一条直线与这条直线平行
③同旁内角相等,两直线平行
④负数没有立方根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (m+n)(-m-n)=m2-n2 | B. | (2a-b)2=4a2-2ab+b2 | ||
| C. | (x+3)(-x+3)=x2-9 | D. | (4x+1)2=16x2+8x+1 |
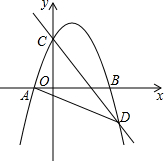 如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-$\frac{3}{2}$x+3交于C、D两点.连接BD、AD.
如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-$\frac{3}{2}$x+3交于C、D两点.连接BD、AD.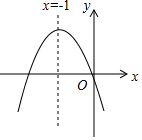 已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=-1,且经过原点.下列结论:(1)b2-4ac>0;(2)a-b+c>0;(3)abc>0(4)b=2a,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图,对称轴为直线x=-1,且经过原点.下列结论:(1)b2-4ac>0;(2)a-b+c>0;(3)abc>0(4)b=2a,其中正确的有( ) 如图,∠BDE=∠EBD,要使AB∥DE,应添加的一个条件是∠ABD=∠EBD(填一个即可)
如图,∠BDE=∠EBD,要使AB∥DE,应添加的一个条件是∠ABD=∠EBD(填一个即可)