题目内容
2. 如图,已知CD是⊙O的直径,AE交⊙O于点B,且AB=OC
如图,已知CD是⊙O的直径,AE交⊙O于点B,且AB=OC(1)若∠EOD=70°,求∠A的度数;
(2)若∠A=20°,∠EOB的度数.
分析 (1)连接OB,由等腰三角形的性质得到∠BOC=∠A,由三角形外角的性质得到∠EBO=2∠A,然后列方程即可得到结论;
(2)由(1)证得∠E=2∠A,根据三角形的外角的性质和三角形的内角和即可得到结论.
解答  解:(1)连接OB,
解:(1)连接OB,
∵AB=OC,
∴AB=OB,
∴∠BOC=∠A,
∴∠EBO=2∠A,
∵OB=OE,
∴∠E=∠EBO=2∠A,
∵∠DOE=∠E+∠A=3∠A=70°,
∴∠A=$\frac{70°}{3}$;
(2)由(1)证得∠E=2∠A,
∵∠A=20°,
∴∠E=40°,
∵∠EBO=∠E=40°,
∴∠EOB=100°.
点评 本题考查了圆周角定理,等腰三角形的性质,三角形的外角的性质,熟练掌握三角形外角的性质定理是解题的关键.

练习册系列答案
相关题目
11.在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
| A. | BD,CE分别为AC,AB上的高 | B. | BD,CE为△ABC的角平分线 | ||
| C. | ∠ABD=$\frac{1}{3}$∠ABC,∠ACE=$\frac{1}{3}$∠ACB | D. | ∠ABD=∠BCE |
12.下列调查中,适宜采用抽样调查方式的是( )
| A. | 对我国首架大型民用直升机各零部件的检查 | |
| B. | 对重庆八中初三某班第一小组的数学成绩的调查 | |
| C. | 对我市市民对“日本准备将我国钓鱼岛非法国有化”这一事件的态度的调查 | |
| D. | 调查乘坐飞机的旅客是否携带了危禁物品 |
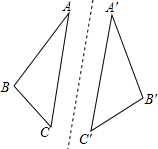 如图,△ABC与△A′B′C′关于直线l对称,对应线段AB和A′B′所在的直线相交吗?另外两组对应线段所在的直线相交吗?如果相交,交点与对称轴l有什么关系?如果不相交,这组对应线段所在直线与对称轴l有什么关系?再找几个成轴对称的图形观察一下,你能发现什么规律?
如图,△ABC与△A′B′C′关于直线l对称,对应线段AB和A′B′所在的直线相交吗?另外两组对应线段所在的直线相交吗?如果相交,交点与对称轴l有什么关系?如果不相交,这组对应线段所在直线与对称轴l有什么关系?再找几个成轴对称的图形观察一下,你能发现什么规律?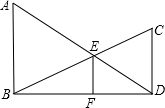 如图,AB⊥BD,CD⊥BD,B、D是垂足,AD和BC交于E,EF⊥BD于F.求证:$\frac{DE}{AD}$+$\frac{BE}{BC}$=1.
如图,AB⊥BD,CD⊥BD,B、D是垂足,AD和BC交于E,EF⊥BD于F.求证:$\frac{DE}{AD}$+$\frac{BE}{BC}$=1.
 一段圆弧形弯道如图,已知l${\;}_{\widehat{BD}}$=50m,l${\;}_{\widehat{AC}}$=30 m,求弯道的中心线$\widehat{EF}$的长.
一段圆弧形弯道如图,已知l${\;}_{\widehat{BD}}$=50m,l${\;}_{\widehat{AC}}$=30 m,求弯道的中心线$\widehat{EF}$的长.