题目内容
2. 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为1.
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为70.4米.(结果精确到0.1米)
分析 A、根据三角形的中位线定理求得DE的长,然后根据FD是直角△ABF斜边上的中线,求得FD的长,则EF即可求得.
B、作出形,可得AB=138米,∠A=24.8°,在Rt△ABC中,利用三角函数即可求得BC的长度.
解答 解:A、∵DE为△ABC的中位线,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5,
∵∠AFB为直角,D是AB的中点,即FD是直角△ABF的中线,
∴FD=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4.
∴EF=DE-FD=5-4=1.
故答案是:1.
B、如图2,在Rt△ABC中,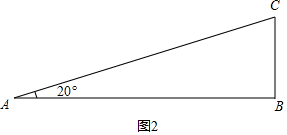
AB=138米,∠BAC=24.8°,
∵$\frac{BC}{AB}$=tan24.8°,
∴BC=ABtan24.8°≈138×0.51≈70,4(米).
故答案为:70.4.
点评 本题考查了三角形的中位线定理以及直角三角形的性质,直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
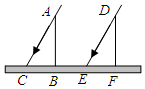 如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )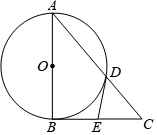 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D的切线交BC于E.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D的切线交BC于E. 如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交
如图,AD、BE是△ABC的两条高,过点D作DF⊥AB,垂足为F,FD交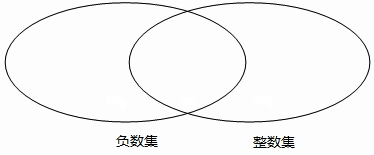 两个圈分别表示负数集合和整数集合,请在每个圈内填入6个数.其中有3个数既是负数,又是整数,这3个数应填在哪里?你能说出这两个圈的重叠部分表示什么数的集合吗?
两个圈分别表示负数集合和整数集合,请在每个圈内填入6个数.其中有3个数既是负数,又是整数,这3个数应填在哪里?你能说出这两个圈的重叠部分表示什么数的集合吗?