题目内容
8.若有方程a2+2015a-1=0与b2+2015b-1=0,则a2b+a2b-ab=2016,1+$\frac{1}{a}$+$\frac{1}{b}$=2016.分析 根据题意,可把a和b看作方程x2+2015x-1=0的两根,根据根与系数的关系得到a+b=-2015,ab=-1,再变形a2b+a2b-ab=ab(a+b-1),1+$\frac{1}{a}$+$\frac{1}{b}$=$\frac{ab+a+b}{ab}$,然后利用整体代入的方法计算.
解答 解:∵方程a2+2015a-1=0与b2+2015b-1=0,
∴a和b看作方程x2+2015x-1=0的两根,
∴a+b=-2015,ab=-1,
∴a2b+a2b-ab=ab(a+b-1)=2016,1+$\frac{1}{a}$+$\frac{1}{b}$=$\frac{ab+a+b}{ab}$=2016.
故答案为:2016,2016.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图,MP=MQ,PN=QN,MN与PQ相交于O,则PQ与MN的关系为( )
如图,MP=MQ,PN=QN,MN与PQ相交于O,则PQ与MN的关系为( )
 如图,MP=MQ,PN=QN,MN与PQ相交于O,则PQ与MN的关系为( )
如图,MP=MQ,PN=QN,MN与PQ相交于O,则PQ与MN的关系为( )| A. | MN=PQ | B. | PQ<MN | C. | MN<PQ | D. | MN⊥PQ |
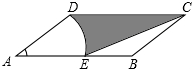 如图,在?ABCD中,BC=10,DC=12,∠B=150°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是55-$\frac{25}{3}$π(结果不取近似值)
如图,在?ABCD中,BC=10,DC=12,∠B=150°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是55-$\frac{25}{3}$π(结果不取近似值)