��Ŀ����
3�����������������ú��������������ҵʱ�����ڡ��������з�ʽ����$\frac{a}{b}•\frac{b}{2a}$����$\frac{y}{x}��\frac{b}{a}$����$\frac{2}{a}��\frac{4}{{a}^{2}}$����$\frac{{x}^{3}}{2y}��\frac{3{x}^{2}}{y}$�������Ƿ�ʽ������Щ���õ��������ֲ�ͬ�Ľ����������ֻ�Т٣�������ֻ�Тڣ����ã��٢ڢۣ�
����Ϊ�����ȷ���ǣ�������
| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ��� |
���� ���ݷ�ʽ�ij˳���������м��㼴�ɣ�
��� �⣺����$\frac{a}{b}•\frac{b}{2a}$=$\frac{1}{2}$Ϊ��ʽ��
��$\frac{y}{x}��\frac{b}{a}$=$\frac{y}{x}•\frac{a}{b}=\frac{ya}{xb}$�Ƿ�ʽ��
��$\frac{2}{a}��\frac{4}{{a}^{2}}$=$\frac{2}{a}•\frac{{a}^{2}}{4}=\frac{a}{2}$����ʽ��
��$\frac{{x}^{3}}{2y}��\frac{3{x}^{2}}{y}$=$\frac{{x}^{3}}{3y}•\frac{y}{3{x}^{2}}$=$\frac{1}{9}$Ϊ��ʽ��
���Ƿ�ʽ��ֻ�Тڣ�
��ѡ��B��
���� ������Ҫ������Ƿ�ʽ�ij˳�����ʽ�Ķ��壬���շ�ʽ�ij˷������������Լ���ʽ�Ķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
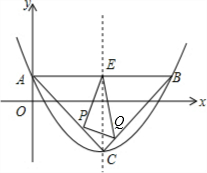 ��C��4��-2��Ϊ����������߽�y���ڵ�A��0��1��������Aƽ����x���ֱ�߽��������ڵ�B���������߶Գ����ڵ�E��
��C��4��-2��Ϊ����������߽�y���ڵ�A��0��1��������Aƽ����x���ֱ�߽��������ڵ�B���������߶Գ����ڵ�E��