题目内容
已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2013个图形中直角三角形的个数有 个.


考点:规律型:图形的变化类
专题:规律型
分析:观察图形可知,两个图形为一个组,直角三角形的个数相同,且都是4的倍数,然后求出第2013个图形的组数,计算即可得解.
解答:解:图①图②的直角三角形的个数相同,都是4,4=4×1,
图③图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013图2014的直角三角形的个数相同,都是4×
=4028.
故答案为:4028.
图③图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013图2014的直角三角形的个数相同,都是4×
| 2014 |
| 2 |
故答案为:4028.
点评:本题是对图形变化规律的考查,观察图形,得到两个图形的直角三角形的个数相同是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,点A是实验中学图书馆所在位置,每天早上9点有一辆洒水车以100米/分的速度从位于A点北偏东30°方向的B处开始沿着杏坛路BC洒水,已知杏坛路位于B点南偏西67°方向,AB的距离为800米,在离洒水车600米的区域内均会受到音乐声的影响.请问:
如图,点A是实验中学图书馆所在位置,每天早上9点有一辆洒水车以100米/分的速度从位于A点北偏东30°方向的B处开始沿着杏坛路BC洒水,已知杏坛路位于B点南偏西67°方向,AB的距离为800米,在离洒水车600米的区域内均会受到音乐声的影响.请问: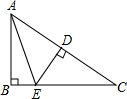 如图,在Rt△ABC中,∠B=90°,DE垂直平分AC,∠BAE:∠EAC=1:2,则∠C=
如图,在Rt△ABC中,∠B=90°,DE垂直平分AC,∠BAE:∠EAC=1:2,则∠C= 已知:如图,一次函数y=-2x的图象与反比例函数y=
已知:如图,一次函数y=-2x的图象与反比例函数y=