题目内容
分解因式:
(1)4x2(a2-25b2)+12xy(25b2-a2)﹢9y2(a2-25b2);
(2)-36a3b2(3a-2b)-24a2b3(2b-3a)
(1)4x2(a2-25b2)+12xy(25b2-a2)﹢9y2(a2-25b2);
(2)-36a3b2(3a-2b)-24a2b3(2b-3a)
考点:提公因式法与公式法的综合运用
专题:
分析:(1)首先提取公因式(a2-25b2),进而利用完全平方公式以及平方差公式分解因式得出即可;
(2)首先提取公因式-12a2b2(3a-2b)(=,进而得出答案.
(2)首先提取公因式-12a2b2(3a-2b)(=,进而得出答案.
解答:解:(1)4x2(a2-25b2)+12xy(25b2-a2)﹢9y2(a2-25b2)
=(a2-25b2)(4x2-12xy+9y2)
=(a+5b)(a-5b)(2x-3y)2;
(2)-36a3b2(3a-2b)-24a2b3(2b-3a)
=-12a2b2(3a-2b)(3a-2b)
=-12a2b2(3a-2b)2.
=(a2-25b2)(4x2-12xy+9y2)
=(a+5b)(a-5b)(2x-3y)2;
(2)-36a3b2(3a-2b)-24a2b3(2b-3a)
=-12a2b2(3a-2b)(3a-2b)
=-12a2b2(3a-2b)2.
点评:此题主要考查了提取公因式法以及公式法分解因式,正确提取公因式是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
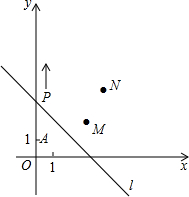 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.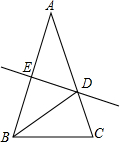 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )