题目内容
1. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B、C两点.已知A(1,0),C(0,3),且BC=5.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B、C两点.已知A(1,0),C(0,3),且BC=5.(1)求B点坐标;
(2)分别求直线BC和抛物线的解析式(关系式).
分析 (1)利用勾股定理得到OB的长,从而可得B点坐标;
(2)把B点和C点坐标代入y=kx+n得到k、n的方程组,然后解方程可确定直线BC的解析式;对于抛物线,可设交点式y=a(x-1)(x-4),然后把C点坐标代入求出a即可.
解答 解:(1)∵C(0,3),
∴OC=3,
在Rt△COB中,∵OC=3,BC=5,∠BOC=90°,
∴OB=$\sqrt{{5^2}-{3^2}}=4$,
∴点B的坐标是(4,0);
(2)∵直线y=kx+n(k≠0)经过B(4,0)、C(0,3)两点,
∴$\left\{\begin{array}{l}{4k+n=0}\\{n=3}\end{array}\right.$,即得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{n=3}\end{array}\right.$
∴直线的解析式为y=-$\frac{3}{4}$x+3;
设抛物线解析式为y=a(x-1)(x-4),
把C(0,3)代入得a•(-1)•(-4)=3,解得a=$\frac{3}{4}$,
∴抛物线解析式为y=$\frac{3}{4}$(x-1)(x-4),即y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3.
点评 本题考查了抛物线与x轴的交点:从y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了待定系数法求函数解析式.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
9.沃美超市某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为( )
| A. | 10% | B. | 20% | C. | ±20% | D. | 30% |
16.“水是生命之源”,某城市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
(1)如果1月份某用户用水量为19m3,那么该用户1月份应该缴纳水费57元.
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
| 用水量/月 | 单价(元/m3) |
| 不超过20m3 | 2.8 |
| 超过20m3的部分 | 3.8 |
| 另:每立方米用水加收0.2元的城市污水处理费 | |
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
13. 如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )
如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )
 如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )
如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )| A. | ∠BDE=120° | B. | ∠ACE=120° | C. | AB=BE | D. | AD=BE |
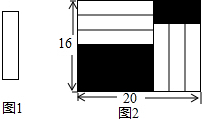 把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是64cm.
把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是64cm.