题目内容
2.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为6.分析 首先根据平均数的定义列出关于a、b的二元一次方程组,再解方程组求得a、b的值,然后求中位数即可.
解答 解:∵两组数据:3,a,2b,5与a,6,b的平均数都是6,
∴$\left\{\begin{array}{l}{a+2b=24-3-5}\\{a+b=18-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=8}\\{b=4}\end{array}\right.$,
若将这两组数据合并为一组数据,按从小到大的顺序排列为3,4,5,6,8,8,8,
一共7个数,第四个数是6,所以这组数据的中位数是6.
故答案为6.
点评 本题考查平均数和中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
7.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别在A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).
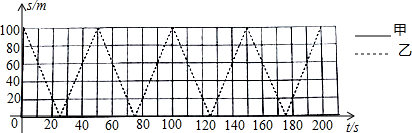
(2)根据(1)中所画图象,完成下列表格:
(3)①直接写出甲、乙两人分别在第一个100m内,t与s的函数解析式,并指出自变量t的取值范围.
②求甲、乙第6次相遇时t的值.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200).

(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数(单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和(单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
②求甲、乙第6次相遇时t的值.
12.在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
根据列表,可以估计出n的值是n=10.
| 摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
| 摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
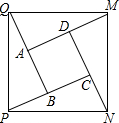 如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.
如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明. 菱形0BCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),当EP+BP最短时,点P的坐标为($2\sqrt{3}-3,2-\sqrt{3}$).
菱形0BCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,-1),当EP+BP最短时,点P的坐标为($2\sqrt{3}-3,2-\sqrt{3}$).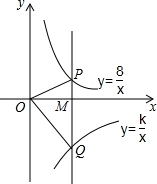 如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为-20.
如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=$\frac{8}{x}$(x>0)和y=$\frac{k}{x}$(x>0)的图象交于P、Q两点,若S△POQ=14,则k的值为-20.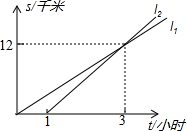 A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是( )
A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/小时;④乙先到达B地.其中正确的个数是( ) 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC=12cm.
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC=12cm.