题目内容
如图，在平面直角坐标系中，矩形OABC，OA=3，OC=6，将△ABC沿对角线AC翻折，使点B落在点B′处，AB′与y轴交于点D，则点D的坐标为 ．
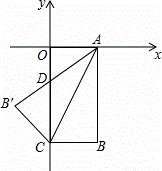
（0，﹣
）： 解：由折叠的性质可知，∠B′AC=∠BAC，
∵四边形OABC为矩形，
∴OC∥AB，
∴∠BAC=∠DCA，
∴∠B′AC=∠DCA，
∴AD=CD，
设OD=x，则DC=6﹣x，在Rt△AOD中，由勾股定理得，
OA2+OD2=AD2，
即9+x2=（6﹣x）2，
解得：x=
，
∴点D的坐标为：（0，
），
故答案为：（0，﹣）．
练习册系列答案
教材全解字词句篇系列答案
相关题目
记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图。
（1）中
命
题的逆命题，如果能补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由。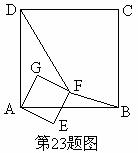
的整数部分是 
≈1.732，结果精确到0.01海里）
，OM平分
，将直角三角板直角的顶点P在射线OM上移动，两直角边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由.