题目内容
4.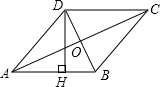 如图,在平行四边形ABCD中,对角线AC⊥BD,且AC=8,BD=6,DH⊥AB于H,则AH等于( )
如图,在平行四边形ABCD中,对角线AC⊥BD,且AC=8,BD=6,DH⊥AB于H,则AH等于( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
分析 易证四边形ABCD是菱形,根据菱形的性质得出BO、CO的长,在RT△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于AB×DH,再利用勾股定理求出AH即可.
解答 解:∵平行四边形ABCD中,AC⊥BD,
∴平行四边形ABCD是菱形,
∴CO=$\frac{1}{2}$AC=3cm,BO=$\frac{1}{2}$BD=4cm,AO⊥BO,
∴BC=5cm,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24cm2,
∵S菱形ABCD=AB×DH,
∴AB×DH=24,
∴DH=$\frac{24}{5}$cm,
∴AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=$\frac{7}{5}$
故选D.
点评 此题考查了菱形的判定与性质,也涉及了勾股定理,要求我们掌握菱形的面积的两种表示方法,及菱形的对角线互相垂直且平分.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
14.已知△ABC中,AB=5,AC=7,BC=a,则a的取值范围是( )
| A. | 1<a<6 | B. | 5<a<7 | C. | 2<a<12 | D. | 10<a<14 |
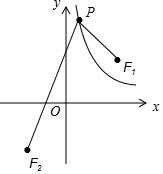 已知直线l1:y=-x+$\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{x}$定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x+$\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{x}$定点F1($\sqrt{2}$k,$\sqrt{2}$k).
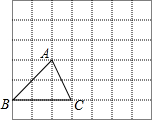 三角形ABC在网格中如图所示,请根据下列提示作图并计算:
三角形ABC在网格中如图所示,请根据下列提示作图并计算: