题目内容
7.若关于x的一元二次方程x2-2x+k-3=0的两个实数根互为倒数,求k的值.分析 根据一元二次方程的定义和根与系数的关系得到:x1•x2=k-3=1,解得k=4.
解答 解:设方程的两根为x1,x2,
∵关于x的一元二次方程x2-2x+k-3=0的两个实数根互为倒数,
∴x1•x2=k-3=1,
∴k=4.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知一元二次方程:2x2-3x-4=0的两个根分别是x1、x2,则x12x2+x1x22的值为( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
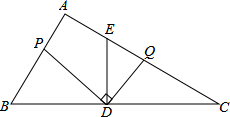 如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.