题目内容
11. 如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB-BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB-BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据点Q的位置分两种情况讨论,当点Q在AB上运动时,求得y与x之间函数解析式,当点Q在BC上运动时,求得y与x之间函数解析式,最后根据分段函数的图象进行判断即可.
解答 解:由题得,点Q移动的路程为2x,点P移动的路程为x,
∠A=∠C=60°,AB=BC=2,
①如图,当点Q在AB上运动时,过点Q作QD⊥AC于D,则
AQ=2x,DQ=$\sqrt{3}$x,AP=x,
∴△APQ的面积y=$\frac{1}{2}$×x×$\sqrt{3}$x=$\frac{\sqrt{3}}{2}{x}^{2}$(0<x≤1),
即当0<x≤1时,函数图象为开口向上的抛物线的一部分,故(A)、(B)排除;
②如图,当点Q在BC上运动时,过点Q作QE⊥AC于E,则
CQ=4-2x,EQ=2$\sqrt{3}$-$\sqrt{3}$x,AP=x,
∴△APQ的面积y=$\frac{1}{2}$×x×(2$\sqrt{3}$-$\sqrt{3}$x)=-$\frac{\sqrt{3}}{2}{x}^{2}$+$\sqrt{3}$x(1<x≤2),
即当1<x≤2时,函数图象为开口向下的抛物线的一部分,故(C)排除,而(D)正确;
故选(D)
点评 本题以动点问题为背景,主要考查了二次函数的图象,函数图象是典型的数形结合,通过看图获取信息,可以提高分析问题、解决问题的能力.解题时注意分类讨论思想的运用.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1.如果$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$是方程ax+(a-2)y=0的一组解,则a的值( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
19. 夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):
夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):
(1)计算夏良该学期数学平时质量检测的平均成绩;
(2)如果学期总评成绩是按照图所示的权重计算,请计算出夏良该学期的数学总评成绩.
 夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):
夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):| 质量检测类型 | 平时 | 期中 | 期末 | |||
| 检测1 | 检测2 | 检测3 | 检测4 | |||
| 成绩 | 90 | 76 | 85 | 89 | 87 | 92 |
(2)如果学期总评成绩是按照图所示的权重计算,请计算出夏良该学期的数学总评成绩.
1.在一个直角三角形中,已知两直角边分别为6cm,8cm,则下列结论不正确的是( )
| A. | 斜边长为10cm | B. | 周长为25cm | ||
| C. | 面积为24cm2 | D. | 斜边上的中线长为5cm |

 如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长交边BC于点D,如果BD=6,那么BC的值为12.
如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长交边BC于点D,如果BD=6,那么BC的值为12.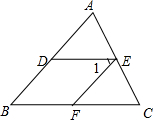 如图,∠AED=∠C,∠1=∠B,说明:EF∥AB
如图,∠AED=∠C,∠1=∠B,说明:EF∥AB