Question

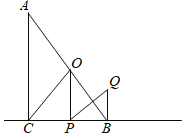
【题目】如图所示，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与B、C重合），连接OC、OP，将OP绕点P顺时针旋转60°，得到线段PQ，连接BQ，若∠BPO＝15°，BP＝4，则BQ的长为_____．

Answer 1

【答案】2+2或4﹣4

【解析】

分两种情况：①当点P在CB延长线上时，连接OQ，证得△OBC是等边三角形得出，由旋转的性质得出△OPQ是等边三角形，得出，推出，由SAS证得得出，证得，过点P作PD⊥BQ于D，则，由勾股定理得出，证得△QDP是等腰直角三角形得出，则；

②当点P在BC延长线上时，连接OQ，证得△OBC是等边三角形得出，推出，由旋转的性质得出△OPQ是等边三角形得出，推出，由SAS证得得出，证得，过点Q作QE⊥BP于E，则，设，则，由勾股定理得出，由等腰直角三角形的性质得出，则，求解即可得出答案．

依题意，分以下两种情况：

①如图1，当点P在CB延长线上时，连接OQ

中，点O为AB中点

∴△OBC是等边三角形

∵OP绕点P顺时针旋转，得到线段PQ

∴△OPQ是等边三角形

在△COP和△BOQ中，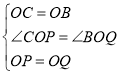

过点P作PD⊥BQ于D，则

∴△QDP是等腰直角三角形

；

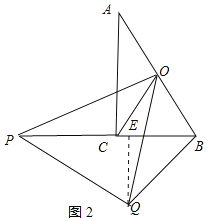
②如图2，当点P在BC延长线上时，连接OQ

中，点O为AB中点

∴△OBC是等边三角形

∵OP绕点P顺时针旋转，得到线段PQ

∴△OPQ是等边三角形

在△COP和△BOQ中，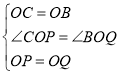

过点Q作QE⊥BP于E，则

设，则

解得，即

综上，BQ的长为或

故答案为：或．