题目内容
11.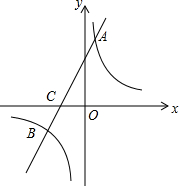 如图,直线y1=ax+b与双曲线y2=$\frac{k}{x}$交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).
如图,直线y1=ax+b与双曲线y2=$\frac{k}{x}$交于A、B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(-3,-2).(1)求直线和双曲线的解析式;
(2)求点C的坐标,并结合图象直接写出y1<0时x的取值范围.
分析 (1)由点B的坐标求出k=6,得出双曲线的解析式为y2=$\frac{6}{x}$.求出A的坐标为(1,6),由点A和B的坐标以及待定系数法即可求出直线的解析式为直线y1=2x+4;
(2)求出点C的坐标为(-2,0),即可得出当y1<0时x的取值范围.
解答 解:(1)∵点B(-3,-2)在双曲线y2=$\frac{k}{x}$上,
∴$\frac{k}{-3}=-2$,
∴k=6,
∴双曲线的解析式为y2=$\frac{6}{x}$.
把y=6代入y2=$\frac{6}{x}$得:x=1,
∴A的坐标为(1,6),
∵直线y1=ax+b经过A、B两点,
∴$\left\{\begin{array}{l}{a+b=6}\\{-3a+b=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$,
∴直线的解析式为直线y1=2x+4;
(2)由直线y1=0得,x=-2,
∴点C的坐标为(-2,0),
当y1<0时x的取值范围是x<-2.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式;熟练掌握待定系数法是解决问题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
1.若一个角为75°,则它的余角的度数为( )
| A. | 285° | B. | 105° | C. | 75° | D. | 15° |
2.小明到商店购买“五四青年节”活动奖品,购买20只铅笔和10本笔记本共需110元,但购买30支铅笔和5本笔记本只需85元,设每支铅笔x元,每本笔记本y元,则可列方程组( )
| A. | $\left\{\begin{array}{l}{20x+30y=110}\\{10x+5y=85}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{20x+10y=110}\\{30x+5y=85}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{20x+5y=110}\\{30x+10y=85}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x+20y=110}\\{10x+30y=85}\end{array}\right.$ |
6.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )
| A. | y=2x2+1 | B. | y=2x2-3 | C. | y=2(x-8)2+1 | D. | y=2(x-8)2-3 |
16.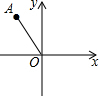 如图,在平面直角坐标系中,点A的坐标为(-1,$\sqrt{3}$),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(-1,$\sqrt{3}$),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
 如图,在平面直角坐标系中,点A的坐标为(-1,$\sqrt{3}$),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
如图,在平面直角坐标系中,点A的坐标为(-1,$\sqrt{3}$),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )| A. | (0,-2) | B. | (1,-$\sqrt{3}$) | C. | (2,0) | D. | ($\sqrt{3}$,-1) |
3.在创建“全国园林城市”期间,郴州市某中学组织共青团员去植树,其中七位同学植树的棵树分别为:3,1,1,3,2,3,2,这组数据的中位数和众数分别是( )
| A. | 3,2 | B. | 2,3 | C. | 2,2 | D. | 3,3 |
20.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $2\sqrt{2}×3\sqrt{2}=6\sqrt{2}$ | C. | $\sqrt{8}÷\sqrt{2}=2$ | D. | $3\sqrt{2}-\sqrt{2}=3$ |