题目内容
 如图所示,A、M、N点坐标分别为A(0,1),M(3,2),N(4,4),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图所示,A、M、N点坐标分别为A(0,1),M(3,2),N(4,4),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.(1)当t=3时,求l的解析式;
(2)若点m,n分别位于l的异侧,试确定t的取值范围.
考点:一次函数图象与几何变换
专题:
分析:(1)当t=3时,由动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,得出P(0,4),那么b=4,进而求出l的解析式;
(2)分别求出直线l经过点M、点N时的t值,即可得到t的取值范围.
(2)分别求出直线l经过点M、点N时的t值,即可得到t的取值范围.
解答:解:(1)当t=3时,∵P(0,4),
∴b=4,
∴y=-x+4;
(2)当直线y=-x+b过点M(3,2)时,
2=-3+b,
解得:b=5,
5=1+t,
解得t=4.
当直线y=-x+b过点N(4,4)时,
4=-4+b,
解得:b=8,
8=1+t,
解得t=7.
故若点M,N位于l的异侧,t的取值范围是:4<t<7.
∴b=4,
∴y=-x+4;
(2)当直线y=-x+b过点M(3,2)时,
2=-3+b,
解得:b=5,
5=1+t,
解得t=4.
当直线y=-x+b过点N(4,4)时,
4=-4+b,
解得:b=8,
8=1+t,
解得t=7.
故若点M,N位于l的异侧,t的取值范围是:4<t<7.
点评:本题考查了一次函数图象与几何变换,一次函数的图象与性质,得出直线l经过点M、点N时的t值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个多项式减x2-y2等于x2+y2,这个多项式为( )
| A、2x2 |
| B、-2x2 |
| C、2y2 |
| D、-2y2 |
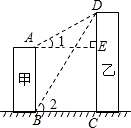 如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从A点测得D点的仰角∠1为30°,从B点测得D点的仰角∠2为60°,已知乙建筑物的高CD=36米.
如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从A点测得D点的仰角∠1为30°,从B点测得D点的仰角∠2为60°,已知乙建筑物的高CD=36米.