题目内容
 如图,AB为⊙O的直径,半径OC⊥AB,D为AB延长线上一点,过D作⊙O的切线,E为切点,连CE交AB于F.
如图,AB为⊙O的直径,半径OC⊥AB,D为AB延长线上一点,过D作⊙O的切线,E为切点,连CE交AB于F.(1)求证:DE=DF;
(2)连AE,若tanC=
| 1 |
| 4 |
考点:切线的性质,圆周角定理,解直角三角形
专题:
分析:(1)连接OE,若要证明DE=DF,则只要证明∠DFE=∠DEF即可;
(2)连BC,过F作BC的垂线,垂足为H,由题意可知△C0B为等腰直角三角形,利用等腰直角三角形的性质和勾股定理,圆周角定理以及已知条件即可求出tanA的值.
(2)连BC,过F作BC的垂线,垂足为H,由题意可知△C0B为等腰直角三角形,利用等腰直角三角形的性质和勾股定理,圆周角定理以及已知条件即可求出tanA的值.
解答:(1)证明:连接OE,
∵半径OC⊥AB,
∴∠COD=90°,
∴∠ OCF+∠CFO=90°
OCF+∠CFO=90°
∵DE是⊙O的切线,E为切点,
∴∠OED=90°,
∴∠OEC+∠FED=90°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OFC=∠FED,
∵∠OFC=∠DFE,
∴∠DFE=∠DEF,
∴DE=DF;
(2)解:连BC,过F作BC的垂线,垂足为H,
∵OC=OB,半径OC⊥AB,
∴∠OCB=∠OBC=45°,
∵若tanC=
,
∴可设OF=1,则OC=4,BF=3,
∴FH=BH=
,BC=4
,
∴HC=BC-BH=4
-
=
,
∴在RT△CFH中,tanA=tan∠HCF=
.
∵半径OC⊥AB,
∴∠COD=90°,
∴∠
 OCF+∠CFO=90°
OCF+∠CFO=90°∵DE是⊙O的切线,E为切点,
∴∠OED=90°,
∴∠OEC+∠FED=90°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OFC=∠FED,
∵∠OFC=∠DFE,
∴∠DFE=∠DEF,
∴DE=DF;
(2)解:连BC,过F作BC的垂线,垂足为H,
∵OC=OB,半径OC⊥AB,
∴∠OCB=∠OBC=45°,
∵若tanC=
| 1 |
| 4 |
∴可设OF=1,则OC=4,BF=3,
∴FH=BH=
3
| ||
| 2 |
| 2 |
∴HC=BC-BH=4
| 2 |
3
| ||
| 2 |
5
| ||
| 2 |
∴在RT△CFH中,tanA=tan∠HCF=
| 3 |
| 5 |
点评:本题考查了圆的切线的性质,等腰三角形的性质和判定等腰直角三角形的性质,勾股定理,圆周角定理以及锐角三角函数,对于考查学生的综合解题能力是一道相当不错的题目.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图所示,图的主视图是( )
如图所示,图的主视图是( )A、 |
B、 |
C、 |
D、 |
 这个直方图回答下面的问题:
这个直方图回答下面的问题: 星期六,同学们可以休息了,有的同学搭顺路的大客车回家,其中一个同学画了一张图如图,由图可判断大客车驶向
星期六,同学们可以休息了,有的同学搭顺路的大客车回家,其中一个同学画了一张图如图,由图可判断大客车驶向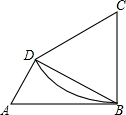 如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为
如图,有一四边形形状的铁皮ABCD,BC=CD=12,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.则该圆锥的底面半径为