题目内容
13.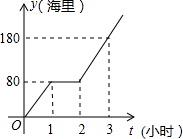 某渔船计划从码头出发到指定海域捕鱼,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该渔船加快速度仍匀速前进,结果恰好准点到达,如图是该渔船行驶的路程y(海里)与所用时间t(小时)的函数图象,则该渔船从码头到捕鱼海域的路程是480海里.
某渔船计划从码头出发到指定海域捕鱼,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该渔船加快速度仍匀速前进,结果恰好准点到达,如图是该渔船行驶的路程y(海里)与所用时间t(小时)的函数图象,则该渔船从码头到捕鱼海域的路程是480海里.
分析 根据函数图象和题意可以求出开始的速度为80海里/时,故障排除后的速度是100海里/时,设计划行驶的路程是a海里,就可以由时间之间的关系建立方程求出路程.
解答 解:由图象及题意,得
故障前的速度为:80÷1=80海里/时,
故障后的速度为:(180-80)÷1=100海里/时.
设航行额全程有a海里,由题意,得
$\frac{a}{80}=2+\frac{a-80}{100}$,
解得:a=480.
故答案为:480.
点评 本题考查了运用函数图象的意义解答行程问题的运用,行程问题的数量关系路程=速度×时间的运用,解答时先根据图象求出速度是关键,再建立方程求出距离是难点.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
3.人体血液中每个成熟红细胞的平均直径为0.0000077米,用科学记数法表示为( )
| A. | 7.7×10-5米 | B. | 77×10-6米 | C. | 77×10-5米 | D. | 7.7×10-6米 |
5.在下列交通标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.如图,观察图形,找出规律,确定第四个图形是( )


| A. |  | B. |  | C. |  | D. |  |
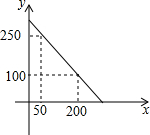 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系式如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.