Question

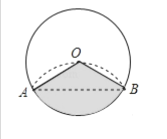
【题目】将半径为3cm的圆形纸片沿AB折叠后，圆弧恰好能经过圆心O，用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为_____．

Answer 1

【答案】cm

【解析】

作OC⊥AB于C，如图，根据折叠的性质得OC等于半径的一半，即OA＝2OC，再根据含30度的直角三角形三边的关系得∠OAC＝30°，则∠AOC＝60°，所以∠AOB＝120°，则利用弧长公式可计算出弧AB的长＝2π，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，得到圆锥的底面圆的半径为1，然后根据勾股定理计算这个圆锥的高．

解：作OC⊥AB于C，如图，

∵将半径为3cm的圆形纸片沿AB折叠后，圆弧恰好能经过圆心O，

∴OC等于半径的一半，即OA＝2OC，

∴∠OAC＝30°，

∴∠AOC＝60°，

∴∠AOB＝120°，

弧AB的长＝＝2π，

设圆锥的底面圆的半径为r，

∴2πr＝2π，解得r＝1，

∴这个圆锥的高＝＝2(cm)，

故答案为：2cm．