Question

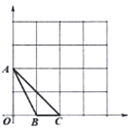
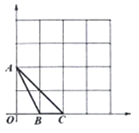
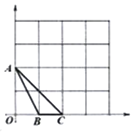
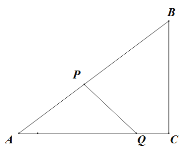
【题目】如图，在等腰中，，AD是的角平分线，且，以点A为圆心，AD长为半径画弧EF，交AB于点E，交AC于点F．

（1）求由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积；

（2）将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高h．

Answer 1

【答案】（1）；（2）.

【解析】

（1）利用等腰三角形的性质得到，，则可计算出，然后利用扇形的面积公式，利用由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积进行计算；（2）设圆锥的底面圆的半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到，解得，然后利用勾股定理计算这个圆锥的高h．

∵在等腰中，，

∴，

∵AD是的角平分线，

∴，，

∴，

∴，

∴由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积.

（2）设圆锥的底面圆的半径为r，

根据题意得，解得，

这个圆锥的高．