题目内容
14. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AD的长为4$\sqrt{3}$cm.
如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AD的长为4$\sqrt{3}$cm.
分析 根据矩形性质得出∠BAD=90°,AO=BO,得出等边三角形AOB,求出∠ABD=60°,在Rt△BAD中,解直角三角形即可求出AD即可.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,AC=2AO,BD=2OB,AC=BD,
∴AO=BO,
∵∠AOB=180°-120°=60°,
∴△AOB是等边三角形,
∴∠ABD=60°,
∴sin60°=$\frac{AD}{BD}$,
∴AD=8cm×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$cm,
故答案为:4$\sqrt{3}$cm.
点评 本题考查了矩形性质,等边三角形的性质和判定,解直角三角形的应用,掌握矩形的对角线相等且互相平分是解题关键.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4. 如图是一个圆柱体,则它的正视图是( )
如图是一个圆柱体,则它的正视图是( )
 如图是一个圆柱体,则它的正视图是( )
如图是一个圆柱体,则它的正视图是( )| A. |  | B. |  | C. |  | D. |  |
5.下列各式中计算正确的是( )
| A. | (-a2)5=-a10 | B. | (x4)3=x7 | C. | b5•b5=b25 | D. | a6÷a2=a3 |
2.实数$\sqrt{4}$,2.$\stackrel{•}{3}$,-2π,$\frac{22}{7}$,$\sqrt{3}$-2,0.030030003,-$\root{3}{9}$中,无理数有( )个.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9. 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )
如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )
 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )
如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )| A. | AC=DF | B. | BE=EC | C. | ∠A=∠D | D. | ∠DEF=90° |
19. 如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )
如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )
 如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )
如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
6.下列计算正确的是( )
| A. | (x+2)(x-2)=x2-2 | B. | (a+b)(b-a)=a2-b2 | C. | (-a+b)2=a2-2ab+b2 | D. | (-a-b)2=a2-2ab+b2 |
3.下列方程中,是二元一次方程的是( )
| A. | 3x-2y=4z | B. | 6xy+9=0 | C. | 4x=$\frac{y-2}{4}$ | D. | $\frac{1}{x}$+4y=6 |
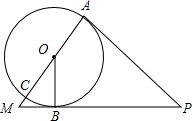 如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.
如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.