题目内容
先阅读,然后解答提出的问题:
设m,n是有理数,且满足m+
n=2-3
,求nm的值.
解:由题意,移项得,(m-2)+(n+3)
=0,
∵m、n是有理数,∴m-2,n+3也是有理数,
又∵
是有理数,∴m-2=0,n+3=0,∴m=2,n=-3
∴nm=(-3)2=9.
问题解决:设a、b都是有理数,且a2+b
=16+5
,求2
-5b的值.
设m,n是有理数,且满足m+
| 5 |
| 5 |
解:由题意,移项得,(m-2)+(n+3)
| 5 |
∵m、n是有理数,∴m-2,n+3也是有理数,
又∵
| 5 |
∴nm=(-3)2=9.
问题解决:设a、b都是有理数,且a2+b
| 2 |
| 2 |
| a |
考点:实数的运算
专题:阅读型
分析:已知等式变形后,根据a与b为有理数,确定出a与b的值,代入原式计算即可得到结果.
解答:解:由题意得:(a2-16)+(b-5)
=0,
∵a,b为有理数,
∴a2-16=0,b-5=0,
解得:a=±4,b=5,
∵a≥0,
∴a=4,
则原式=2×2-5×5=4-25=-21.
| 2 |
∵a,b为有理数,
∴a2-16=0,b-5=0,
解得:a=±4,b=5,
∵a≥0,
∴a=4,
则原式=2×2-5×5=4-25=-21.
点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
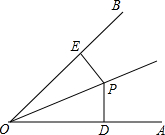 如图,∠POB=∠POA,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )
如图,∠POB=∠POA,PD⊥OA于D,PE⊥OB于E,下列结论错误的是( )| A、PD=PE |
| B、OD=OE |
| C、PD=OD |
| D、∠DPO=∠EPO |
方程x2+4x-1=0的左边配成完全平方后所得方程为( )
| A、(x+2)2=5 |
| B、(x-2)2=5 |
| C、(x+4)2=9 |
| D、(x-4)2=9 |
计算:(-2)3+(-3)2的结果是( )
| A、1 | B、-1 | C、0 | D、17 |
用代数式表示“a的3倍与b的差”是( )
| A、3a-b |
| B、3a+b |
| C、a3-b |
| D、a-3b |