题目内容
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在边AB上,点Q在边BC上,且BQ=x,AP=2x(0<x<5),连接PQ.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在边AB上,点Q在边BC上,且BQ=x,AP=2x(0<x<5),连接PQ.(1)设△BPQ的面积为y,当x为何值时,y的值最大,最大值是多少?
(2)当x为何值时,△BPQ与△ABC相似.
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)过P作PD⊥BC于点D,利用x表示出PD,则可表示出△BPQ的面积,再利用二次函数求得其最大值;
(2)利用x表示出BQ和BP,分∠PQB=90°和∠QPB=90°分别利用相似三角形的对应边成比例可求得x.
(2)利用x表示出BQ和BP,分∠PQB=90°和∠QPB=90°分别利用相似三角形的对应边成比例可求得x.
解答:解:(1)过P作PD⊥BC于点D,如图,
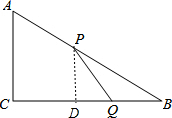
∵∠C=90°,AC=6,BC=8,
∴AB=10,
又∵BQ=x,AP=2x,
∴PB=10-2x,
∵PD∥AC,
∴
=
,
即
=
,
∴PD=6-
,
∴y=
BQ•PD=
x(6-
x)=-
x2+3x,
该二次函数开口向下,当x=
时y有最大值,最大值为
;
(2)∵∠PBQ=∠CBA,∠C=90°,
∴当△BPQ与△ABC相似时有两种情况,
①当∠PQB=90°时,则有
=
,即
=
,解得x=
;
②当∠QPB=90°时,则有
=
,即
=
,解得x=
;
综上可知,当x为
或
时,△BPQ与△ABC相似.

∵∠C=90°,AC=6,BC=8,
∴AB=10,
又∵BQ=x,AP=2x,
∴PB=10-2x,
∵PD∥AC,
∴
| PQ |
| AC |
| PB |
| AB |
即
| PD |
| 6 |
| 10-2x |
| 10 |
∴PD=6-
| 6x |
| 5 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 5 |
| 3 |
| 5 |
该二次函数开口向下,当x=
| 5 |
| 2 |
| 15 |
| 4 |
(2)∵∠PBQ=∠CBA,∠C=90°,
∴当△BPQ与△ABC相似时有两种情况,
①当∠PQB=90°时,则有
| BP |
| AB |
| BQ |
| BC |
| 10-2x |
| 10 |
| x |
| 8 |
| 40 |
| 13 |
②当∠QPB=90°时,则有
| BP |
| BC |
| BQ |
| AB |
| 10-2x |
| 8 |
| x |
| 10 |
| 25 |
| 7 |
综上可知,当x为
| 40 |
| 13 |
| 25 |
| 7 |
点评:本题主要考查相似三角形的判定和性质及二次函数的最值,掌握相似三角形的对应边成比例是解题的关键,注意分类讨论思想的应用.

练习册系列答案
相关题目
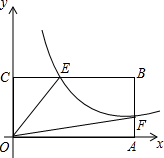 如图,矩形OABC的边OA,OC分别在x轴和y轴上,点B的坐标为(6,3),双曲线y=
如图,矩形OABC的边OA,OC分别在x轴和y轴上,点B的坐标为(6,3),双曲线y=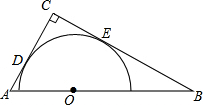 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则CD为
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则CD为