题目内容
已知:P是△ABC内任意一点,连接PA,求AB+BC+AC与PA+PB+PC的关系.
考点:三角形三边关系
专题:
分析:根据题意画出图形,再根据三角形的三边关系可得出结论.
解答: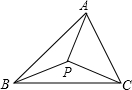 解:PA+PB+PC>
解:PA+PB+PC>
(AB+BC+AC).
理由:如图所示,在△ABP中,AP+BP>AB.
同理:BP+PC>BC,AP+PC>AC.
以上三式分别相加得到:
2(PA+PB+PC)>AB+BC+AC,即PA+PB+PC>
(AB+BC+AC).
 解:PA+PB+PC>
解:PA+PB+PC>| 1 |
| 2 |
理由:如图所示,在△ABP中,AP+BP>AB.
同理:BP+PC>BC,AP+PC>AC.
以上三式分别相加得到:
2(PA+PB+PC)>AB+BC+AC,即PA+PB+PC>
| 1 |
| 2 |
点评:本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边是解答此题的关键.

练习册系列答案
相关题目
 一位同学想利用树影测量树高,他在某一时间测得长为1m的竹竿影长0.8m,但当他马上测量树影时,因树靠近一幢建筑物,影子不完全落在地面上,有一部分影子在墙上,如图所示,他先测得留在墙上的影高为1.2m,又测得地面部分的影长为5m,测算一下这棵树的高时多少?
一位同学想利用树影测量树高,他在某一时间测得长为1m的竹竿影长0.8m,但当他马上测量树影时,因树靠近一幢建筑物,影子不完全落在地面上,有一部分影子在墙上,如图所示,他先测得留在墙上的影高为1.2m,又测得地面部分的影长为5m,测算一下这棵树的高时多少? 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在边AB上,点Q在边BC上,且BQ=x,AP=2x(0<x<5),连接PQ.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在边AB上,点Q在边BC上,且BQ=x,AP=2x(0<x<5),连接PQ.