题目内容
4.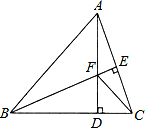 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,AD=BD,AD与BE交于点F,连接CF,求证:BF=2AE.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,AD=BD,AD与BE交于点F,连接CF,求证:BF=2AE.
分析 求出∠ADC=∠BDF,∠DAC=∠DBF,根据ASA推出△BDF≌△ADC,根据全等得出AC=BF,根据等腰三角形的性质求出AC=2AE,即可得出答案.
解答 证明:∵BE⊥AC,AD⊥BC,
∴∠AEB=∠ADC=∠BDF=90°,
∵∠AFE=∠BFD,∠FBD+∠BDF+∠BFD=180°,∠AEB+∠AFE+∠DAC=180°,
∴∠DAC=∠DBF,
在△BDF和△ADC中
$\left\{\begin{array}{l}{∠FBD=∠DAC}\\{BD=AD}\\{∠BDF=∠ADC}\end{array}\right.$
∴△BDF≌△ADC,
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AE=CE,
即AC=2AE,
∴BF=2AE.
点评 本题考查了全等三角形的性质和判定和等腰三角形的性质,能求出△BDF≌△ADC是解此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
3.在-4、-2、0、1、3、4这六个数中,正数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
 如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )
如图,在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么BF:CF等于( )| A. | 5:8 | B. | 3:8 | C. | 3:5 | D. | 2:5 |
16.二次函数y=(x-m)2-m2-1有最小值-4,则实数m的值可能是( )
| A. | -$\sqrt{3}$ | B. | -3 | C. | $\sqrt{5}$ | D. | 4 |
 用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )
用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )



 如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)
如图,线段AB=2n,点P是线段AD上的动点(不包括端点),分别以AP.BP为斜边,在线段AB两侧作等腰Rt△ACP和等腰Rt△BDP,则C、D两点之间的距离为$\sqrt{2}$n.(用含n的代数式表示)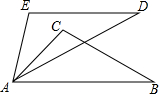 如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.
如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是85°.