题目内容
某船在A、B地之间航行,顺水航行需要4小时,逆水航行需要5小时,水流速度为2千米/时.
(1)求船在静水中的速度;
(2)若船从A地顺水航行到B地,然后逆流返回,到达距离A地26千米的C地,一共航行了多少小时?
(1)求船在静水中的速度;
(2)若船从A地顺水航行到B地,然后逆流返回,到达距离A地26千米的C地,一共航行了多少小时?
考点:一元一次方程的应用
专题:
分析:(1)首先设船在静水中的速度是x千米/时,根据逆水时间×逆水速度=顺水时间×顺水速度可得方程,再解方程即可.
(2)需要分类讨论:点A在点C的上游和下游两种情况.
(2)需要分类讨论:点A在点C的上游和下游两种情况.
解答: 解:(1)设船在静水中的速度是x千米/时,由题意得:
解:(1)设船在静水中的速度是x千米/时,由题意得:
4(x+2)=5(x-2),
解得:x=18.
答:船在静水中的速度18千米/时;
(2)设由B到C航行时间为t.
如图1,当点A在点C的上游时,
4×(18+2)-26=(18-2)t,
解得 t=
,
则一共所需的时间为:4+
=
(小时);
如图2,当点A在点C的下游时,4×(18+2)+26=(18-2)t,
解得 t=
,
则一共所需的时间为:4+
=
(小时);
答:一共航行所用的时间是
小时或
小时.
 解:(1)设船在静水中的速度是x千米/时,由题意得:
解:(1)设船在静水中的速度是x千米/时,由题意得:4(x+2)=5(x-2),
解得:x=18.
答:船在静水中的速度18千米/时;
(2)设由B到C航行时间为t.
如图1,当点A在点C的上游时,
4×(18+2)-26=(18-2)t,
解得 t=
| 27 |
| 8 |
则一共所需的时间为:4+
| 27 |
| 8 |
| 59 |
| 8 |
如图2,当点A在点C的下游时,4×(18+2)+26=(18-2)t,
解得 t=
| 53 |
| 8 |
则一共所需的时间为:4+
| 53 |
| 8 |
| 85 |
| 8 |
答:一共航行所用的时间是
| 59 |
| 8 |
| 85 |
| 8 |
点评:此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系列出方程.

练习册系列答案
相关题目
在平面直角坐标系xOy中,以M(3,4)为圆心,半径为5的圆与x轴的位置关系是( )
| A、相离 | B、相交 |
| C、相切 | D、无法确定 |
如果a的相反数是6,那么a等于( )
| A、6 | ||
B、
| ||
C、-
| ||
| D、-6 |
 如图,P为⊙O的直径AB的延长线上一点,PC切⊙O于点C,若∠P=26°,则∠A等于( )
如图,P为⊙O的直径AB的延长线上一点,PC切⊙O于点C,若∠P=26°,则∠A等于( )| A、32° | B、36° |
| C、38° | D、42° |
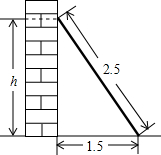 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h.