题目内容
19. 如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.
如图,在直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,0)、B(3,6)、C(10,8)、D(13,0),确定这个四边形的面积.
分析 过点B作BE⊥x轴于点E,过点C作CF⊥x轴于点F,根据点B、C的坐标可得出点E、F的坐标,利用分割图形求面积法即可求出四边形ABCD的面积.
解答 解:过点B作BE⊥x轴于点E,过点C作CF⊥x轴于点F,如图所示.
∴点E(3,0),点F(10,0),
∴S四边形ABCD=S△BAE+S梯形BEFC+S△CFD=$\frac{1}{2}$AE•BE+$\frac{1}{2}$(BE+CF)•EF+$\frac{1}{2}$CF•DF=$\frac{1}{2}$×3×6+$\frac{1}{2}$×(6+8)×7+$\frac{1}{2}$×8×3=70.
点评 本题考查了坐标与图形性质、三角形的面积以及梯形的面积,将不规则的四边形ABCD分割成直角三角形以及直角梯形是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
9. 如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为( )
如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为( )
 如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为( )
如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
4.不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集中任何x的值均在2≤x≤5的范围内,则a的取值范围是( )
| A. | a≥2 | B. | 2≤a≤4 | C. | a≤4 | D. | a≥2且a≠4 |

 已如抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,-$\frac{1}{2}$)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
已如抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,-$\frac{1}{2}$)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
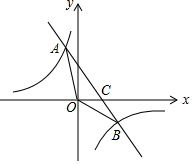 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A的坐标为(-3,n),线段OB=10,且sin∠BOC=$\frac{3}{5}$.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A的坐标为(-3,n),线段OB=10,且sin∠BOC=$\frac{3}{5}$. 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.求证:
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.求证: