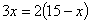题目内容
已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
【考点】根的判别式;根与系数的关系.
【专题】计算题.
【分析】(1)先计算出△=(m+2)2﹣4(2m﹣1),变形得到△=(m﹣2)2+4,由于(m﹣2)2≥0,则△>0,然后根据△的意义得到方程有两个不相等的实数根;
(2)利用根与系数的关系得到x1+x2=0,即m+2=0,解得m=﹣2,则原方程化为x2﹣5=0,然后利用直接开平方法求解.
【解答】(1)证明:△=(m+2)2﹣4(2m﹣1)
=m2﹣4m+8
=(m﹣2)2+4,
∵(m﹣2)2≥0,
∴(m﹣2)2+4>0,
即△>0,
所以方程有两个不相等的实数根;
(2)设方程的两个根为x1,x2,由题意得:
x1+x2=0,即m+2=0,解得m=﹣2,
当m=﹣2时,方程两根互为相反数,
当m=﹣2时,原方程为x2﹣5=0,
解得:x1=﹣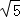 ,x2=
,x2=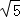 .
.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程和根与系数的关系.

练习册系列答案
相关题目
 N,NH交∠CDG的平
N,NH交∠CDG的平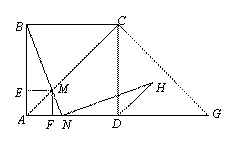
 的值.
的值.

 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.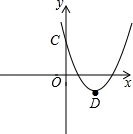
 ,当函数值y随x的增大而减小时,x的取值范围是( )
,当函数值y随x的增大而减小时,x的取值范围是( )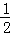 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.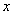 台机械运土,这里
台机械运土,这里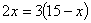 B.
B.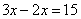 C.
C.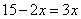 D.
D.