题目内容
如图，A、B分别为y=x2上两点，且线段AB⊥y轴，若AB=6，则直线AB的表达式为( )
A．y=3 B．y=6 C．y=9 D．y=36
C【考点】二次函数图象上点的坐标特征．
【专题】计算题．
【分析】根据抛物线的对称性可知B点的横坐标为3，代入抛物线解析式可求B点的纵坐标，从而可得直线AB的表达式．
【解答】解：∵线段AB⊥y轴，且AB=6，
∴由抛物线的对称性可知，B点横坐标为3，
当x=3时，y=x2=32=9，
∴直线AB的表达式y=9．
故选C．
【点评】本题考查了抛物线的对称性与点的坐标的关系，关键是根据对称性求B点的横坐标．
练习册系列答案
相关题目
，AD是∠BAC的平分线，若P、Q分别是AD和AC的动点，则PC+PQ的最小值是 ． 
．7个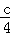
=0的根的情况是( )