题目内容
已知二次函数y=x2﹣2mx+m2﹣1(m≠0)的图象经过点(1,0).
(1)求二次函数的解析式;
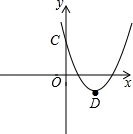
(2)该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
( 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)把点(1,0)代入y=x2﹣2mx+m2﹣1,解方程求出m的值即可;
(2)令x=0,得y=3,即可得出C点坐标.将抛物线解析式配方成顶点式,即可得出顶点D的坐标;
(3)由两点之间线段最短知PC+PD≤CD,得出当C,P,D三点共线时,PC+PD最短.由待定系数法求出直线CD的解析式,即可求出点P坐标.
【解答】解:(1)把点(1,0)代入y=x2﹣2mx+m2﹣1,
得:12﹣2m+m2﹣1=0,
解得:m=2,或m=0(不合题意,舍去),
∴m=2,
∴二次函数的解析式为y=x2﹣4x+3;
(2)令x=0,得y=3,
∴C点坐标为(0,3).
将y=x2﹣4x+3配方得:y=(x﹣2)2﹣1,
∴D点坐标为(2,﹣1).
(3)存在;点P的坐标为(1.5,0).理由如下:
由两点之间线段最短知PC+PD≤CD,
∴当C,P,D三点共线时,PC+PD最短.
设直线CD的解析式为y=kx+b,
根据题意得: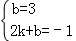 ,
,
解得:k=﹣2,b=3,
直线CD的解析式为:y=﹣2x+3,
当y=0时,x=1.5,
∴点P的坐标为(1.5,0).
【点评】本题是二次函数综合题目,考查了二次函数解析式的求法、一次函数解析式的求法、抛物线的顶点坐标、抛物线与y轴的交点、最短线段问题等知识;本题综合性强,有一定难度,确定二次函数和一次函数解析式是解决问题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目


 .7个
.7个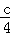 =0的根的情况是( )
=0的根的情况是( ) 4.70千克 B.25.30千克 C.24.80千克 D.25.51千克
4.70千克 B.25.30千克 C.24.80千克 D.25.51千克 DCE
DCE , 则
, 则