题目内容
4. 如图是用棋子摆成的“T”字图案.从图案中可以看出,第1个“T”字型图案需要5枚棋子,第2个“T”字型图案需要8枚棋子,第3个“T”字型图案需要11枚棋子.
如图是用棋子摆成的“T”字图案.从图案中可以看出,第1个“T”字型图案需要5枚棋子,第2个“T”字型图案需要8枚棋子,第3个“T”字型图案需要11枚棋子.(1)照此规律,摆成第8个图案需要26枚棋子?
(2)摆成第n个图案需要3n+2枚棋子?
(3)摆成第2013个图案需要6041枚棋子?
分析 (1)通过观察已知图形可得:每个图形都比其前一个图形多3枚棋子,得出摆成第八个图案需要的棋子数;
(2)由(1)得出规律为摆成第n个图案需要3n+2枚棋子;
(3)由(2)中规律求出即可.
解答 解:(1)第1个“T”字型图案需要3+2=5枚棋子,
第2个“T”字型图案需要3×2+2=8枚棋子,
第3个“T”字型图案需要3×3+2=11枚棋子,
…
第n个图案需要3n+2枚棋子.
那么当n=8时,则有26枚;
故摆成第8个图案需要26枚棋子.
(2)第n个图案需3n+2枚棋子.
(3)3×2013+2=6041(枚),
即第2013个图案需6041枚棋子.
故答案为:26;3n+2;6041.
点评 此题主要考查了图形的变化规律,注意由特殊到一般的分析方法,得出数字变化规律是解题关键.

练习册系列答案
相关题目
17.把正比例函数y=2x的图象向下平移3个单位后,所得图象的函数关系式为( )
| A. | y=2(x-3) | B. | y=2x-3 | C. | y=2x+3 | D. | y=2x |
13.下列各式从左到右的变形中,属于因式分解的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | a2+2ab+b2=(a+b)2 | C. | a(a+b)=a2+ab | D. | (a-b)2=(b-a)2 |
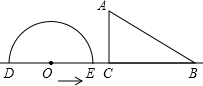 如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角形的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.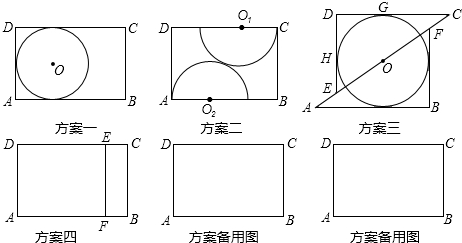
 如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.
如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.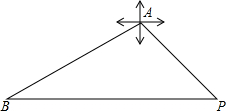 北京时间2014年3月8日凌晨1时20分,由马来西亚飞往北京的马来西亚航空公司MH370航班于地面失去联系,机上239人中包括153名中国大陆乘客.飞机可能出事的海域在点P的正西方向且距离P约2000海里的点B处,中国海上搜救中心的海警船3411在点A观测P点在东偏南45度方向,观测飞机疑似“终结”区域点B在点A的西偏南30度方向,海警船点A到疑似出事区域点B的距离.
北京时间2014年3月8日凌晨1时20分,由马来西亚飞往北京的马来西亚航空公司MH370航班于地面失去联系,机上239人中包括153名中国大陆乘客.飞机可能出事的海域在点P的正西方向且距离P约2000海里的点B处,中国海上搜救中心的海警船3411在点A观测P点在东偏南45度方向,观测飞机疑似“终结”区域点B在点A的西偏南30度方向,海警船点A到疑似出事区域点B的距离.