题目内容
20.已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,(1)求a的取值范围;
(2)在(1)中选择一个合适的a,求代数式(1-$\frac{1}{a-1}$)$÷\frac{{a}^{2}-4a+4}{{a}^{2}-1}$ 的值.
分析 (1)根据一元二次方程的定义和判别式的意义得到a-1≠0且△=(-2)2-4(a-1)>0,然后解两个不等式得到它们的公共部分即可;
(2)首先化简分式,进一步选择一个合适的a的值,代入求得答案即可.
解答 解:(1)∵一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,
∴a-1≠0且△=(-2)2-4(a-1)>0,
解得a<2且a≠1.
(2)原式=$\frac{a-2}{a-1}$•$\frac{(a+1)(a-1)}{(a-2)^{2}}$
=$\frac{a+1}{a-2}$,
当a=$\frac{1}{2}$时,
原式=-1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义与分式的化简求值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12.下来各数中,比-1小的数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -$\sqrt{2}$ |
 数a,b,c在数轴上的位置如图所示,化简|a-c|+|b-c|+|a+b|.
数a,b,c在数轴上的位置如图所示,化简|a-c|+|b-c|+|a+b|.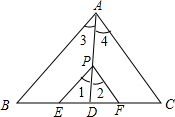 如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.