题目内容
5.解方程(组)(1)4(x-2)2-(3x-1)2=0
(2)$\left\{\begin{array}{l}{x-2y=1}\\{x-y=2-2y}\end{array}\right.$
(3)$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1.
分析 (1)根据平方差公式,可分解因式,可得方程的解;
(2)根据加减消元法,可得方程组的解;
(3)根据等式的性质,可得整式方程,根据解整式方程,可得答案.
解答 解:(1)因式分解,得
[2(x-2)+(3x-1)][2(x-2)-(3x-1)]=0,
化简,得
(5x-5)(x+3)=0,
于是,得
5x-5=0,x+3=0,
解得x=1,x=-3;
(2)化简方程组,得
$\left\{\begin{array}{l}{x-2y=1\\;①}\\{x+y=2②}\end{array}\right.$,
①-②,得
-3y=-1,
解得y=$\frac{1}{3}$,
把y=$\frac{1}{3}$代入②,得
x=$\frac{5}{3}$,
原方程组的解为$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=\frac{1}{3}}\end{array}\right.$;
(3)方程两边都乘以(x-3),得
2-x-1=x-3,
解得x=2,
经检验:x=2是原分式方程的解.
点评 本题考查了因式分解法解一元二次方程,(1)因式分解是解题关键;(2)加减消元法是解题关键;(3)把分式方程转化成整式方程是解题关键,注意要检验.

练习册系列答案
相关题目
14.一次函数y=-x+3的图象经过坐标系的( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
 如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.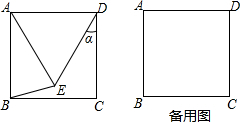
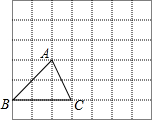 如图,已知三角形ABC,请根据下列提示作图:
如图,已知三角形ABC,请根据下列提示作图: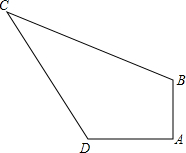 有一块四边形的花坛ABCD,其中AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求这块花坛的面积.
有一块四边形的花坛ABCD,其中AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求这块花坛的面积.