题目内容
2. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°,OA=3,则阴影部分面积为9$\sqrt{3}$-3π.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°,OA=3,则阴影部分面积为9$\sqrt{3}$-3π.
分析 根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,进一步求得∠APB的度数,然后根据阴影部分的面积等于四边形OAPB的面积减去扇形AOB的面积即可求得.
解答  解:∵在△ABO中,OA=OB,∠OAB=30°,
解:∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°-2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,∠APB=360°-120°-90°-90°=60°.
连接OP.
根据切线长定理得∠APO=30°,
∴OP=2OA=6,AP=OP•cos30°=3$\sqrt{3}$,∠AOP=60°.
∴四边形的面积=2S△AOP=2×$\frac{1}{2}$×3×3$\sqrt{3}$=9$\sqrt{3}$;扇形的面积是$\frac{120π×{3}^{2}}{360}$=3π,
∴阴影部分的面积是9$\sqrt{3}$-3π.
故答案为9$\sqrt{3}$-3π.
点评 本题考查了切线长定理、切线的性质定理以及30°的直角三角形的性质.关键是熟练运用扇形的面积计算公式,能够把四边形的面积转化为三角形的面积计算..

练习册系列答案
相关题目
5.我县某地2016年元旦的最高气温为7℃,最低气温为-2℃,那么该地这天的最高气温比最低气温高( )
| A. | -9℃ | B. | -5℃ | C. | 5℃ | D. | 9℃ |
 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2,其中正确结论的个数是( ) 如图,已知线段AB的长为a,延长线段AB至点C,使BC=$\frac{1}{2}AB$.
如图,已知线段AB的长为a,延长线段AB至点C,使BC=$\frac{1}{2}AB$.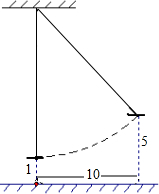 如图所示,有一架绳索拉直的秋千,当它静止时,踏板与地面的距离为1尺;将它往前推进10尺,踏板与地面的距离就为5尺.
如图所示,有一架绳索拉直的秋千,当它静止时,踏板与地面的距离为1尺;将它往前推进10尺,踏板与地面的距离就为5尺.