题目内容
2、当-1≤x≤2时，式子2+|x-2|的最大值为
5
．分析：根据x的取值范围求得|x-2|的最大值，然后求得式子2+|x-2|即可．
解答：解：∵-1≤x≤2，
∴当x=-1时，|x-2|=|-1-2|=|-3|=3，
当x=2时，|x-2|=|2-2|=0，
∴2+|x-2|的最大值为2+3=5．
故答案为：5．
∴当x=-1时，|x-2|=|-1-2|=|-3|=3，
当x=2时，|x-2|=|2-2|=0，
∴2+|x-2|的最大值为2+3=5．
故答案为：5．
点评：本题考查了函数的最值问题，解决本题时根据x的取值，确定绝对值的最大值是解题的关键．
练习册系列答案
相关题目
如图所示，在直角坐标系中，点A是反比例函数y1=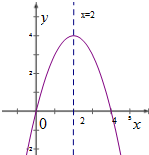
二次函数y=-x2+bx+c的图象如图所示，下列几个结论：
后, 有以下四个判断, 其中错误的是
；
；
；……你能总结出
等于
.
等于
.并求出当n＝300时上式的值
．