题目内容
12．
已知：如图，在?ABCD中，AE：EB=1：3，则FE：FC=（ ）| A． | 1：2 | B． | 2：3 | C． | 3：4 | D． | 3：2 |
分析 根据AE：EB以及平行四边形对边相等求出EB：CD，再求出△BEF和△DCF相似，根据相似三角形对应边成比例解答．
解答 解：∵AE：EB=1：3，
∴EB：AB=3：4，
在?ABCD中，AB=CD，
所以，EB：CD=3：4，
∵?ABCD对边AB∥CD，
∴△BEF∽△DCF，
∴FE：FC=EB：CD=3：4．
故选C．
点评 本题考查了相似三角形的判定与性质，平行四边形的性质，难点在于根据已知条件求出EB：AB的值．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
3．下列各式-$\frac{1}{2}$mn，m，8，$\frac{1}{a}$，x2+2x+6，$\frac{2x-y}{5}$，$\frac{{x}^{2}+4y}{π}$，$\frac{1}{y}$中，整式有（ ）
| A． | 3个 | B． | 4个 | C． | 6个 | D． | 7个 |
7．若8x3ym÷4xny2=2y2，则m，n的值为（ ）
| A． | m=1，n=3 | B． | m=4，n=3 | C． | m=4，n=2 | D． | m=3，n=4 |
17．下列各数中，是无理数的是（ ）
| A． | $\sqrt{2}$ | B． | $\root{3}{8}$ | C． | $\sqrt{16}$ | D． | $\frac{1}{3}$ |
4．
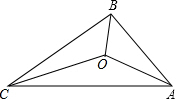如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S△OAB：S△OBC：S△OAC=（ ）
如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S△OAB：S△OBC：S△OAC=（ ）| A． | 1：1：1 | B． | 1：2：3 | C． | 2：3：4 | D． | 3：4：5 |