题目内容
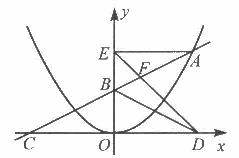
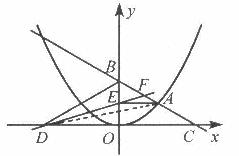
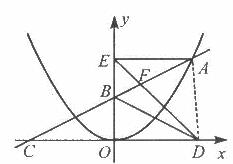
如图,在平面直角坐标系中,A是抛物线 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当 时,求S的值.
时,求S的值.
(2)求S关于 的函数解析式.
的函数解析式.
(3)①若S= 时,求
时,求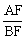 的值;
的值;
②当m>2时,设 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.

(1)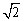 ;(2)
;(2)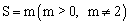 ;(3)①
;(3)①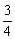 ;②
;②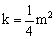 ,证明见解析.
,证明见解析.
【解析】(1)∵点A是抛物线 上的一个动点,AE⊥y轴于点E,且
上的一个动点,AE⊥y轴于点E,且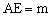 ,
,
∴点A的坐标为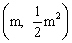 .∴当
.∴当 时,点A的坐标为
时,点A的坐标为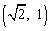 .
.
∵点B的坐标为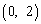 ,∴BE=OE=1.
,∴BE=OE=1.
∵AE⊥y轴,∴AE∥x轴. ∴△ABE∽△CBO.∴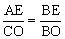 ,即
,即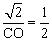 ,解得
,解得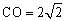 .
.
∵点D与点C关于y轴对称,∴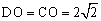 .
.
∴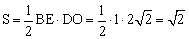 .
.
(2)①当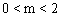 时,如图,
时,如图,
∵点D与点C关于y轴对称,∴△DBO≌△CBO.
∵△ABE∽△CBO,∴△ABE∽△DBO .∴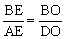 .∴
.∴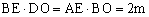
∴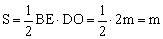 .
.
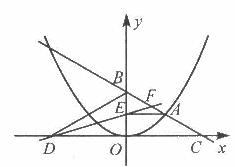
②当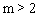 时,如图,同①可得
时,如图,同①可得
综上所述,S关于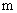 的函数解析式
的函数解析式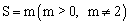 .
.
(3)①如图,连接AD,
∵△BED的面积为 ,∴
,∴ .∴点A 的坐标为
.∴点A 的坐标为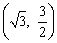 .
.
设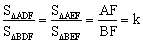 ,∴
,∴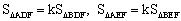 .
.
∴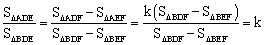 .
.
∴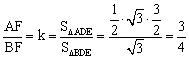 .
.
②k与m的数量关系为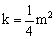 ,证明如下:
,证明如下:
连接AD,则
∵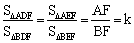 ,∴
,∴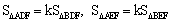 .
.
∴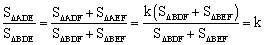 .
.
∵点A 的坐标为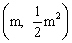 ,∴
,∴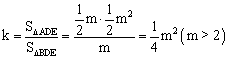 .
.

练习册系列答案
相关题目
 的周长为
的周长为 ,
, ,垂足为
,垂足为 ,
, ,则下列结论正确的有( )
,则下列结论正确的有( ) ;②
;② ;③菱形面积为
;③菱形面积为 ;
; .
. 个 B.
个 B. 个 C.
个 C. 个 D.
个 D. 个
个

 与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D. 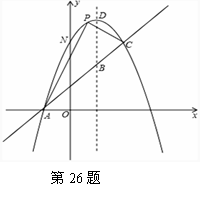
 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
 ,其中
,其中 .
. B
B ;
; B
B 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
 和
和 是同类项,则
是同类项,则 、
、 的值是( )
的值是( ) ,
, B.
B. ,
,
 ,
, D.
D. ,
,