题目内容
1. 如图,△ABC中,∠ABC=70°,∠C=50°,AD⊥BC于点D,且AE平分∠BAC.
如图,△ABC中,∠ABC=70°,∠C=50°,AD⊥BC于点D,且AE平分∠BAC.(1)则∠BAC=60°;
(2)求∠DAE的度数;
(3)过点B作BF⊥AC于点F,交AE于点G,若GF=1cm,AB=4cm,求△ABG的面积.
分析 (1)根据三角形内角和定理计算即可;
(2)根据角平分线的性质求出∠BAE的度数,根据直角三角形的性质求出∠BAD的度数,计算即可;
(3)作GH⊥AB于H,根据角平分线的性质求出GH,根据三角形的面积公式计算即可.
解答 解:(1)∵∠ABC=70°,∠C=50°,
∴∠BAC=180°-70°-50°=60°,
故答案为:60°;
(2)∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=30°,
∵AD⊥BC,∠ABC=70°,
∴∠BAD=20°,
∴∠DAE=10°;
(3)作GH⊥AB于H,
∵AE平分∠BAC,GH⊥AB,BF⊥AC,
∴GH=GF=1cm,又AB=4cm,
∴△ABG的面积=$\frac{1}{2}$×AB×GH=2cm2.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
12.由上饶到南昌的某一次列车,运行途中停靠的车站依次是:上饶-横峰-弋阳-贵溪-鹰潭-余江-东乡-莲塘-南昌,那么要为这次列车制作的火车票有( )
| A. | 9种 | B. | 18种 | C. | 36种 | D. | 72种 |
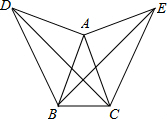 如图所示,在△ABC中,AB=AC,分别以AB,AC为直角边向外作两个等腰直角三角形△ABD和△ACE,使∠BAD=∠CAE=90°,求证:BE=CD.
如图所示,在△ABC中,AB=AC,分别以AB,AC为直角边向外作两个等腰直角三角形△ABD和△ACE,使∠BAD=∠CAE=90°,求证:BE=CD.