Question

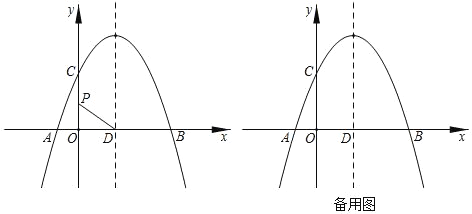
【题目】如图，抛物线y=mx2-2mx-3m（m＞0）与x轴交于A、B两点，与y轴交于点C，点M为抛物线的顶点，且OC=OB．

（1）求抛物线的解析式．

（2）若抛物线上有一点P，连PC交线段BM于Q点，且S△BPQ=S△CMQ，求P点的坐标．

（3）把抛物线沿x轴正半轴平移n个单位，使平移后的抛物线交直线BC于E、F两点，且E、F关于点B对称，求n的值．

Answer 1

【答案】（1）45°；（2）P（2，﹣1），PB=;(3) m＝或﹣．

【解析】

（1）先求出点A、B的坐标、OB、OC的长，从而得到点C的坐标，然后把点C的坐标代入抛物线的解析式就可解决问题；

（2）运用待定系数法可求得直线BC的解析式为y=x-3，由S△BPQ=S△CMQ可得S△PBC=S△MBC，从而可得MP∥BC，故直线MP的解析式可设为y=x+n，然后只需求出抛物线y=x2-2x-3的顶点M的坐标，就可得到直线MP的解析式为y=x-5，最后求得直线MP与抛物线的交点坐标即可；

（3）设平移后抛物线的解析式：y=（x-1-n）2-4，将y=x-3代入y=（x-1-n）2-4得：x-3=（x-1-n）2-4，从而可得到xE+xF=2n+3，依据依据点E与点F关于B对称可得到2n+3=6，从而可求得n的值．

（1）令y=0，得：mx2-2mx-3m=0，

∵m＞0，

∴x2-2x-3=0，

解得：x1=-1，x2=3，

∴A（-1，0）、，B（3，0）、OB=3．

∵OC=OB=3，点C在y轴的负半轴上，

∴C（0，-3），

∴-3m=-3，

∴m=1，

∴抛物线的解析式为y=x2-2x-3．

（2）设直线BC的解析式为y=kx+b，则有，

解得：，

∴直线BC的解析式为y=x-3．

∵S△BPQ=S△CMQ，

∴S△BPQ+S△BCQ=S△CMQ+S△BCQ，

∴S△PBC=S△MBC，

∴MP∥BC，

∴直线MP的解析式可设为y=x+n．

∵抛物线y=x2-2x-3=（x-1）2-4的顶点M的坐标为（1，-4），

∴1+n=-4，

∴n=-5，

∴直线MP的解析式为y=x-5．

联立，解得：（舍去），或，

∴点P的坐标为（2，-3）．

（3）平移后抛物线的解析式：y=（x-1-n）2-4．

将y=x-3代入y=（x-1-n）2-4得：x-3=（x-1-n）2-4，整理得：x2-（2n+3）x+（n+1）2-1=0，

∴xE+xF=2n+3．

又∵点E与点F关于点B对称，

∴xE+xF=2×3，即2n+3=6，解得：n=．