题目内容
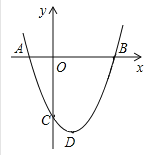
【题目】已知抛物线与x轴相交于两点A(1,0),B(-3,0),与y轴相交于点C(0,3)．
(1)求此抛物线的函数表达式;
(2)如果点
是抛物线上的一点,求△ABD的面积．
【答案】（1）抛物线的解析式为y=﹣（x﹣1）（x+3）（或y=﹣x2﹣2x+3）;（2）△ABD的面积是
．
【解析】
试题（1）设抛物线的解析式为
. 将A、B两点坐标代入抛物线的解析式中，即可求出待定系数的值，从而确定该二次函数的解析式；
（2）将D点横坐标代入抛物线的解析式中，即可求出m的值；以AB为底，D点纵坐标的绝对值为高，即可求出△ABD的面积．
试题解析：
解：(1)∵抛物线与y轴相交于点C(0，3),
∴设抛物线的解析式为.
∵抛物线与x轴相交于两点
，
∴
解得：
∴抛物线的函数表达式为：
.
（2）∵点
是抛物线上一点，
∴
.
∴
.
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
